مطالب تدریس شده در کلاس
- در شکل زیر، مقادیر \(x\) و \(y\) چقدر است؟
-
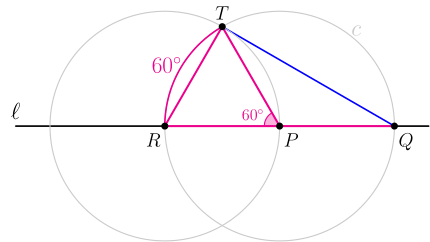
نقطه‌های $P$ و $Q$ روی خط $\ell$ مفروض‌اند. به مرکز $P$ و شعاع $PQ$ دایرهٔ $c$ را رسم کرده‌ایم؛ این دایره خط $\ell$ را در نقطهٔ $R$ قطع می‌کند. به مرکز $R$ و شعاع $RP$ دایرهٔ دیگری رسم می‌کنیم تا دایرهٔ $c$ را در نقطهٔ $T$ قطع کند. اندازهٔ زاویهٔ $RQT$ چند درجه است؟
راه‌حل اول
مثلث \(PRT\) مثلث متساوی‌الاضلاع است(؟). پس \(R\widehat{P}T=60^\circ\). چون زاویهٔ \(RPT\) زاویهٔ مرکزی است، پس کمان \(RT\) برابر (60) درجه است.
از طرفی، زاویهٔ \(RQT\) یک زاویهٔ محاطی است که کمان روبه‌رو به آن، کمان \(RT\) است. بنابراین:
\[\begin{aligned}R\widehat{Q}T&=\frac{\overset{\frown}{RT}}{2}\\[7pt]&=\frac{60^\circ}{2}\\[7pt]&=30^\circ.\end{aligned}\]راه‌حل دوم
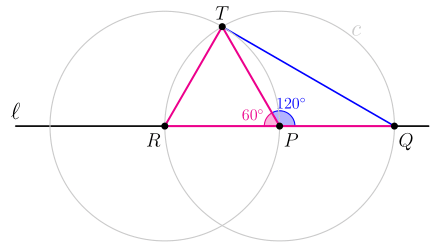
مثلث \(PRT\) مثلث متساوی‌الاضلاع است(؟). پس \(R\widehat{P}T=60^\circ\). در نتیجه \(T\widehat{P}Q=120^\circ\).
چون \(PQ\) و \(PT\) هر دو شعاع دایرهٔ \(c\) هستند، پس مثلث \(PQT\) متساوی‌الساقین است. در نتیجه:
\[Q\widehat{T}P=T\widehat{Q}P=30^\circ.\]این سؤال با توجه به مسئلهٔ ۳ مرحلهٔ بتا طرح شده است.
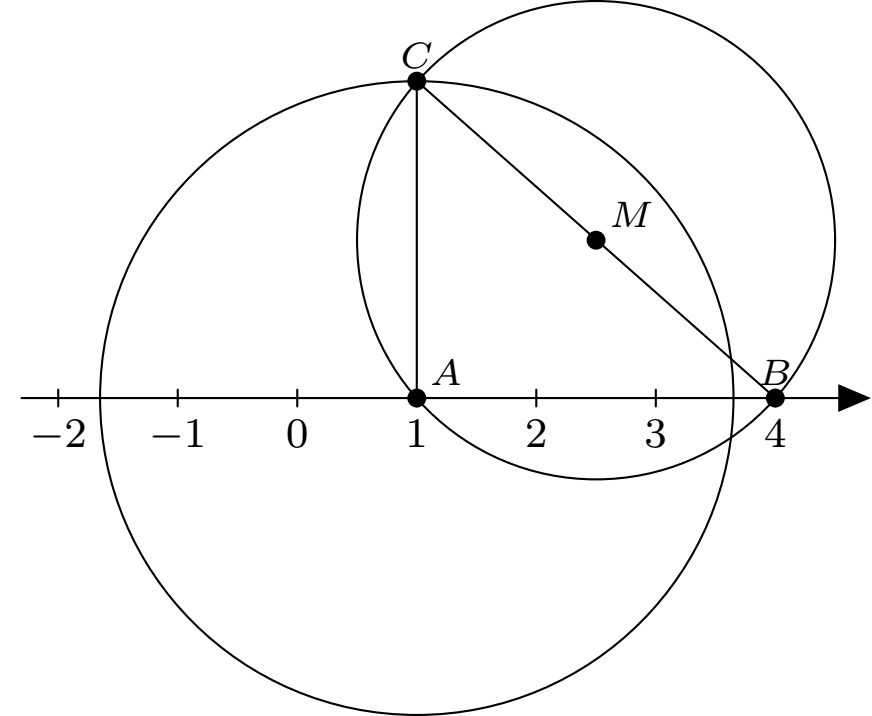
- رضا روی محور اعداد صحیح، نقاط $A$ و $B$ را به‌ترتیب متناظر با اعداد $1$ و $4$ در نظر گرفت. او به مرکز $M$ دایره‌ای به شعاع $2$ رسم کرد؛ این دایره محور اعداد را در نقاط $A$ و $B$ قطع کرد.رضا پاره‌خط $BM$ را امتداد داد تا دایره را در نقطهٔ $C$ قطع کند. سپس به مرکز $A$ و شعاع $AC$ دایرهٔ دیگری رسم کرد؛ این دایره در چه نقاطی محور اعداد را قطع می‌کند؟
واضح است که نقطه $M$ روی محور اعداد قرار ندارد. چون $BM$ شعاع و $BC$ قطر دایرهٔ اول (دایرهٔ به مرکز $M$) است پس بنابه قضیهٔ زاویهٔ محاطی، زاویهٔ $BAC$ قائمه و در نتیجه مثلث $ABC$ قائم‌الزاویه است. اکنون قضیهٔ فیثاغورس را در مثلث $ABC$ به‌کار می‌گیریم:
\[\begin{aligned}&AB^2+AC^2=BC^2\\&\Rightarrow AC^2=BC^2-AB^2\\&\Rightarrow AC^2=4^2-3^2\\&\Rightarrow AC^2=16-9\\&\Rightarrow AC=\sqrt{7}.\end{aligned}\] بنابراین دایرهٔ دوم (دایرهٔ به مرکز $A$) محور اعداد را در نقاط $1-\sqrt{7}$ و $1+\sqrt{7}$ قطع می‌کند.
- در مثلث $ABC$ نقطهٔ $D$ روی ضلع $BC$ چنان قرار دارد که $AD=BD=CD$. اگر $AD=2$ و $AC=3$ آنگاه طول $AB$ را بیابید.
- در شکل زیر، اگر $AB=AC=BD$، و $AC$ بر $BD$ عمود باشد، آنگاه اندازهٔ $\widehat{C}+\widehat{D}$ چقدر است؟
- در شکل زیر، نقطه‌های \(E\) و \(F\) به‌ترتیب روی پاره‌خط‌های \(AB\) و \(AD\) قرار دارند. نقطهٔ \(G\) محل برخورد پاره‌خط‌های \(AC\) و \(BD\) است. همچنین، پاره‌خط‌های \(AG\)، \(BF\)، و \(DE\) یکدیگر را در نقطهٔ \(H\) قطع کرده‌اند.
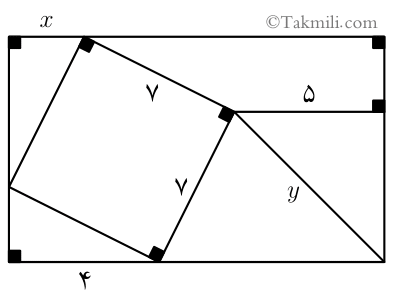
ابتدا شکل داده شده را به‌صورت زیر نام‌گذاری می‌کنیم.
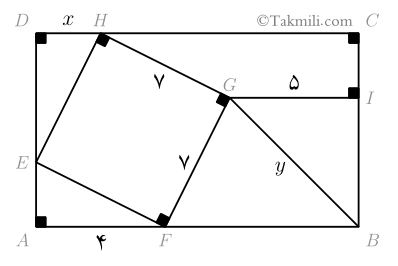چهارضلعی $EFGH$ مربع است.در چهارضلعی $EFGH$، بنابه فرض مسئله، سه زاویه قائمه هستند. چون مجموع زاویه‌های این چهارضلعی \(360\) درجه است پس اندازه زاویهٔ چهارم \(90\) درجه است. می‌دانیم اگر در یک چهارضلعی همهٔ زاویه‌ها قائمه باشند آن چهارضلعی مستطیل است. پس $EFGH$ مستطیل است. از طرفی، چون طول و عرض $EFGH$ برابر \(7\) است پس $EFGH$ مربع است.
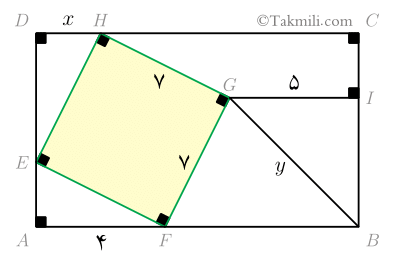پس $EF=7$ و در نتیجه:
\[AE=\sqrt{33}\quad (1)\]
با به‌کارگیری قضیهٔ فیثاغورس در مثلث $AEF$ داریم:
\[\begin{aligned}&AE^2+AF^2=EF^2\\&\Rightarrow AE^2+4^2=7^2\\&\Rightarrow AE^2+16=49\\&\Rightarrow AE^2=49-16\\&\Rightarrow AE^2=33\\&\Rightarrow AE=\sqrt{33}.\end{aligned}\]
برای سادگی قرار می‌دهیم:
\[\begin{aligned}A\widehat{E}F&=w\quad (2)\\D\widehat{E}H&=z.\quad (3)\end{aligned}\]
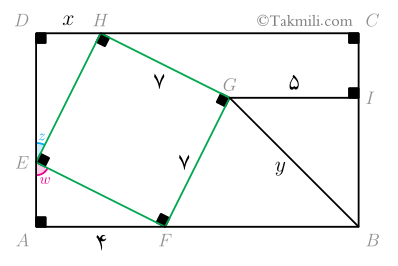دراین‌صورت داریم:
\[w+z=90^\circ\quad (4)\]
چون $EFGH$ مربع است، پس $F\widehat{E}H=90^\circ$. بنابه رابطه‌های (۲) و (۳) داریم:
\[\begin{aligned}&A\widehat{E}F+F\widehat{E}H+D\widehat{E}H=180^\circ\\&\Rightarrow w+90^\circ+z=180^\circ\\&\Rightarrow w+z=180^\circ-90^\circ\\&\Rightarrow w+z=90^\circ.\end{aligned}\]
بنابراین:
\[\begin{aligned}E\widehat{F}A&=z\quad(5)\\E\widehat{H}D&=w.\quad (6)\end{aligned}\]
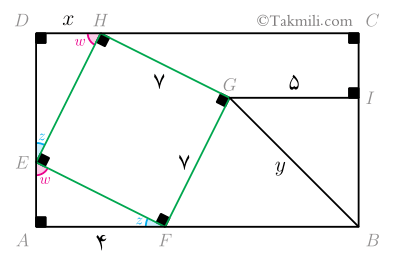
ابتدا ثابت می‌کنیم $E\widehat{F}A=z$.
بنابه فرض مسئله ($E\widehat{A}F=90^\circ$)، قضیهٔ مجموع زاویه‌های مثلث (در مثلث $AEF$)، و رابطهٔ \((2)\) داریم:
\[\begin{aligned}&E\widehat{A}F+A\widehat{E}F+E\widehat{F}A=180^\circ\\&\Rightarrow 90^\circ+w+E\widehat{F}A=180^\circ\\&\Rightarrow w+E\widehat{F}A=180^\circ-90^\circ\\&\Rightarrow w+E\widehat{F}A=90^\circ.\end{aligned}\]
از رابطهٔ بالا و رابطهٔ \((4)\) نتیجه میشود:
\[\left.\begin{aligned}w+E\widehat{F}A=90^\circ\\w+z=90^\circ\end{aligned}\right\}\Rightarrow E\widehat{F}A=z.\]
در ادامه ثابت می‌کنیم $E\widehat{H}D=w$.
بنابه فرض مسئله ($E\widehat{D}H=90^\circ$)، قضیهٔ مجموع زاویه‌های مثلث (در مثلث $DEH$)، و رابطهٔ \((3)\) داریم:
\[\begin{aligned}&E\widehat{D}H+D\widehat{E}H+E\widehat{H}D=180^\circ\\&\Rightarrow 90^\circ+z+E\widehat{H}D=180^\circ\\&\Rightarrow z+E\widehat{H}D=180^\circ-90^\circ\\&\Rightarrow z+E\widehat{H}D=90^\circ.\end{aligned}\]
از رابطهٔ بالا و رابطهٔ \((4)\) نتیجه میشود:
\[\left.\begin{aligned}z+E\widehat{H}D=90^\circ\\w+z=90^\circ\end{aligned}\right\}\Rightarrow E\widehat{H}D=w.\]
پس دو مثلث $AEF$ و $DHE$ در حالت زض‌ز هم‌نهشت‌اند.
چون چهارضلعی $EFGH$ مربع است، پس $EF=EH$.
بنابه رابطه‌های \((3)\) و \((5)\) داریم $E\widehat{F}A=D\widehat{E}H=z$.
بنابه رابطه‌های \((2)\) و \((6)\) داریم $A\widehat{E}F=E\widehat{H}D=w$.
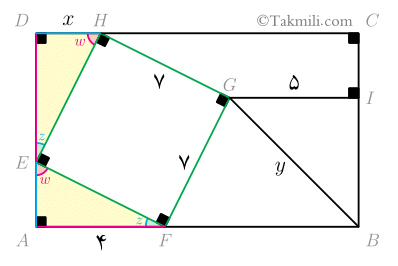
بنابراین
\[x=\sqrt{33}\quad(\star)\]
از هم‌نهشتی دو مثلث $AEF$ و $DHE$ نتیجه میشود $AE=DH$. پس بنابه رابطهٔ \((1)\) و فرض مسئله داریم:
\[\left.\begin{aligned}AE=DH\\AE=\sqrt{33}\\DH=x\end{aligned}\right\}\Rightarrow x=\sqrt{33}.\]
اگر از $G$ خطی بر $AB$ عمود کنیم و پای عمود را $J$ بنامیم، آنگاه دو مثلث $AEF$ و $JFG$ در حالت ززض هم‌نهشت هستند.
$A\widehat{E}F=F\widehat{G}J=w$ (؟).
$E\widehat{A}F=G\widehat{J}F=90^\circ$.
$EF=FG$ (؟).
در نتیجه:
\[AF=GJ=4\quad (7)\]
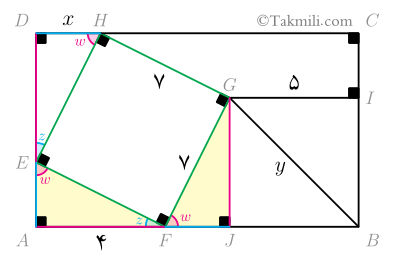از طرفی، چهارضلعی $BIGJ$ مستطیل است.(؟)
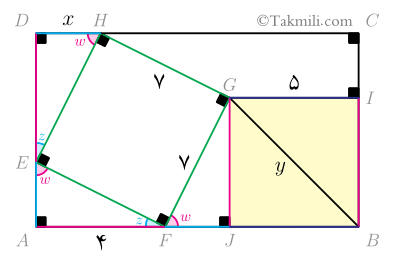
بنابراین:
\[y=\sqrt{41}\quad (*)\]
چون $BIGJ$ مستطیل است، پس
\[GI=JB=5\quad (8)\]
حال بنابه رابطه‌های (۷) و (۸) و با به‌کارگیری قضیهٔ فیثاغورس در مثلث $BGJ$ داریم:
\[\begin{aligned}&y^2=GJ^2+JB^2\\&\Rightarrow y^2=4^2+5^2\\&\Rightarrow y^2=16+25\\&\Rightarrow y^2=41\\&\Rightarrow y=\sqrt{41}.\end{aligned}\]
چون مثلث‌های \(ADB\) و \(ADC\) متساوی‌الساقین هستند. در نتیجه، بنابه قضیهٔ مثلث متساوی‌الساقین، هریک از این مثلث‌ها یک جفت زاویهٔ برابر دارند. برای سادگی، این زاویه‌های برابر را با \(x\) و \(y\) نمایش می‌دهیم.
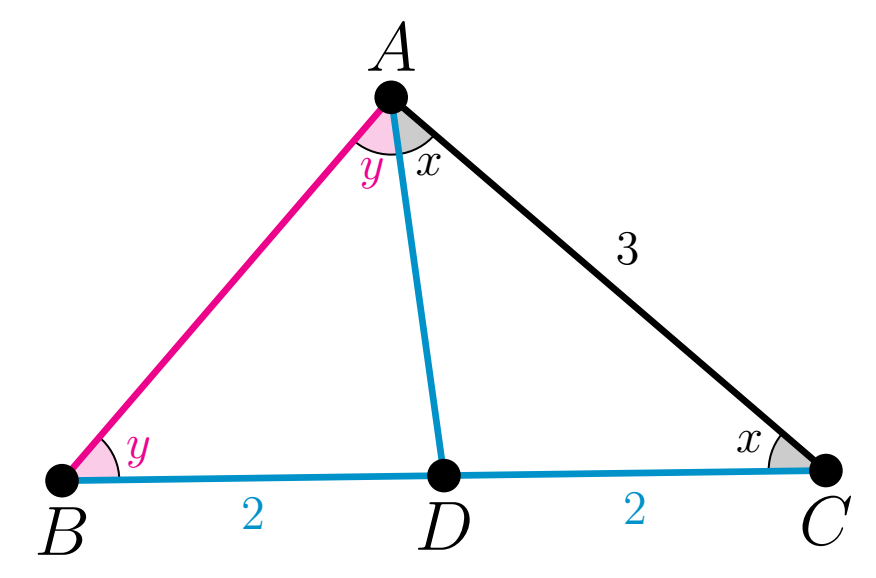
\[\begin{aligned}&D\widehat{A}C=D\widehat{C}A=x\\&D\widehat{B}A=D\widehat{A}B=y.\end{aligned}\] حال، بنابه قضیهٔ مجموع زاویه‌های مثلث، در مثلث \(ABC\) داریم:
\[\begin{aligned}&B\widehat{A}C+\widehat{B}+\widehat{C}=180^\circ\\&\Rightarrow(x+y)+y+x=180^\circ\\&\Rightarrow2x+2y=180^\circ\\&\Rightarrow2(x+y)=180^\circ\\&\Rightarrow x+y=90^\circ.\end{aligned}\] بنابراین، مثلث \(ABC\) قائم‌الزاویه است. پس بنابه قضیهٔ فیثاغورس داریم:
\[\begin{aligned}&AB^2+AC^2=BC^2\\&\Rightarrow AB^2+3^2=4^2\\&\Rightarrow AB^2=16-9\\&\Rightarrow AB=\sqrt{7}.\end{aligned}\]
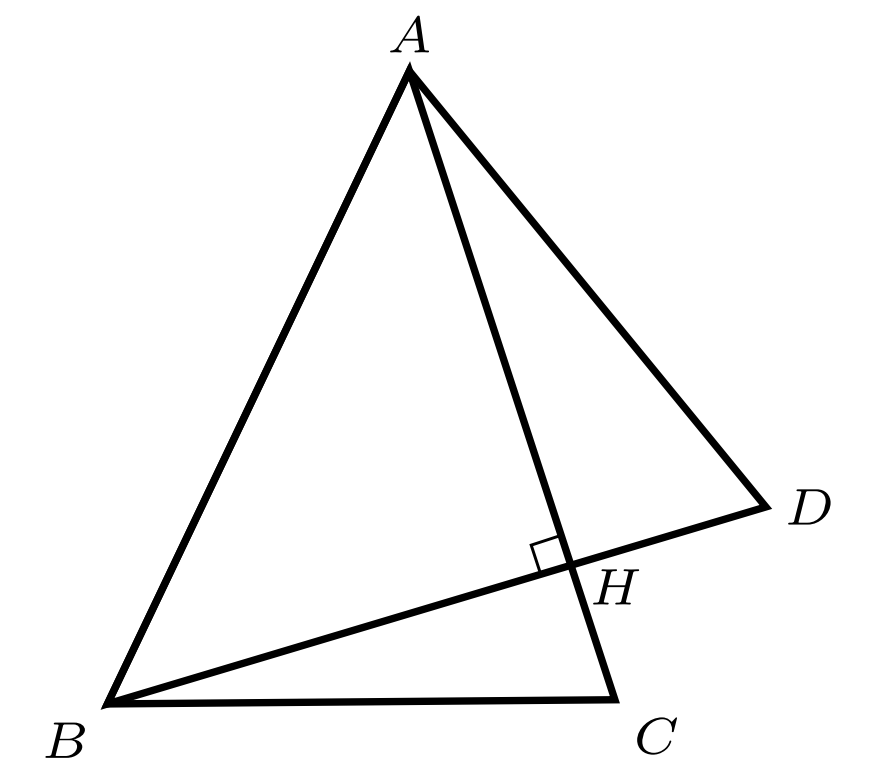
ابتدا برای سادگی، زاویه‌های شکل را به‌صورت زیر نام‌گذاری می‌کنیم.
چون \(AB=AC\)، پس بنابه قضیهٔ مثلث متساوی‌الساقین، داریم:
\[\widehat{C}=x+z.\quad(1)\]
چون \(AB=BD\)، پس بنابه قضیهٔ مثلث متساوی‌الساقین، داریم:
\[\widehat{D}=y+t.\quad(2)\]
از رابطه‌های \((1)\) و \((2)\) نتیجه میشود:
\[\begin{aligned}\widehat{C}+\widehat{D}=x+z+y+t.\quad(3)\end{aligned}\]
از طرفی، بنابه قضیهٔ مجموع زاویه‌های مثلث، در مثلث \(ABC\)، داریم:
\[\widehat{C}=180^\circ-(y+x+z).\quad(4)\]
همچنین، بنابه قضیهٔ مجموع زاویه‌های مثلث، در مثلث \(AHD\)، داریم:
\[\widehat{D}=90^\circ-t.\quad(5)\]
از رابطه‌های \((4)\)، \((5)\)، و \((3)\) نتیجه میشود:
\[\begin{aligned}&\widehat{C}+\widehat{D}=180^\circ-(y+x+z)+90^\circ-t\\&\Rightarrow\widehat{C}+\widehat{D}=270^\circ-(y+x+z+t)\\&\Rightarrow\widehat{C}+\widehat{D}=270^\circ-(\widehat{C}+\widehat{D})\\&\Rightarrow 2(\widehat{C}+\widehat{D})=270^\circ\\&\Rightarrow \widehat{C}+\widehat{D}=135^\circ.\end{aligned}\]
اگر \(x\) یک عدد باشد و
\(\bullet\) مساحت مثلث \(AFH\) برابر \(4x+4\)،
\(\bullet\) مساحت مثلث \(DFH\) برابر \(2x+20\)،
\(\bullet\) مساحت مثلث \(DGH\) برابر \(5x+20\)،
\(\bullet\) مساحت مثلث \(CDG\) برابر \(5x+11\)،
\(\bullet\) مساحت مثلث \(BCG\) برابر \(8x+32\)،
\(\bullet\) و مساحت مثلث \(BGH\) برابر \(8x+50\) باشد،
آن‌وقت مجموع مساحت مثلث‌های \(AEH\) و \(BEH\) چقدر است؟
راهنمایی:با استفاده از ایده‌ای که در اثبات قضیهٔ میانه-مساحت وجود دارد، به‌سادگی می‌توان قضیهٔ بالا را ثابت کرد.
در راه‌حل زیر، بارها از قضیهٔ میانه-مساحت استفاده خواهیم کرد.
برای سادگی، مساحت مثلث‌های \(BGH\)، \(DGH\)، \(BCG\)، و \(CDG\) را به‌ترتیب با \(k\)، \(t\)، \(m\)، و \(n\) نمایش می‌دهیم.
با استفاده از قضیهٔ میانه-مساحت در مثلث‌های \(BDH\) و \(BCD\) داریم:
\[\frac{k}{t}=\frac{m}{n}.\quad(1)\]
با استفاده از قضیهٔ میانه-مساحت در مثلث \(BDH\) داریم:
\[\frac{k}{t}=\frac{BG}{DG}\quad(2)\]
همچنین، با استفاده از قضیهٔ میانه-مساحت در مثلث \(BCD\) داریم:
\[\frac{m}{n}=\frac{BG}{DG}\quad(3)\]
از رابطه‌های \((2)\) و \((3)\) نتیجه میشود:
\[\frac{k}{t}=\frac{m}{n}.\]
از رابطهٔ \((1)\) نتیجه میشود که \(x=5\).
با توجه به رابطهٔ \((1)\) داریم:
\[\begin{aligned}&\frac{S_{\overset{\triangle}{BGH}}}{S_{\overset{\triangle}{DGH}}}=\frac{S_{\overset{\triangle}{BCG}}}{S_{\overset{\triangle}{DCG}}}\\[12pt]&\Rightarrow\frac{8x+50}{5x+20}=\frac{8x+32}{5x+11}\\[8pt]&\Rightarrow(8x+50)(5x+11)=(5x+20)(8x+32)\\&\Rightarrow40x^2+88x+250x+550=40x^2+160x+160x+640\\&\Rightarrow338x+550=320x+640\\&\Rightarrow338x-320x=640-550\\&\Rightarrow18x=90\\&\Rightarrow x=5.\end{aligned}\]
بنابراین:
\[\begin{aligned}S_{\overset{\triangle}{AFH}}&=4x+4=4(5)+4=24\\[5pt]S_{\overset{\triangle}{DFH}}&=2x+20=2(5)+20=30\\[5pt]S_{\overset{\triangle}{DGH}}&=5x+20=5(5)+20=45\\[5pt]S_{\overset{\triangle}{BGH}}&=8x+50=8(5)+50=90.\end{aligned}\]
در نتیجه:
\[\begin{aligned}\frac{BG}{DG}=2.\quad(4)\end{aligned}\]
پس
\[S_{\overset{\triangle}{ABH}}=108.\quad(5)\]
با استفاده از قضیهٔ میانه-مساحت در مثلث \(ABD\)، و رابطهٔ \((4)\) داریم:
\[\begin{aligned}&\frac{S_{\overset{\triangle}{ABG}}}{S_{\overset{\triangle}{ADG}}}=\frac{BG}{DG}\\[14pt]&\Rightarrow\frac{S_{\overset{\triangle}{AEH}}+S_{\overset{\triangle}{BEH}}+S_{\overset{\triangle}{BGH}}}{S_{\overset{\triangle}{AFH}}+S_{\overset{\triangle}{DFH}}+S_{\overset{\triangle}{DGH}}}=2\\[14pt]&\Rightarrow\frac{S_{\overset{\triangle}{AEH}}+S_{\overset{\triangle}{BEH}}+90}{24+30+45}=2\\[14pt]&\Rightarrow\frac{S_{\overset{\triangle}{AEH}}+S_{\overset{\triangle}{BEH}}+90}{99}=2\\[7pt]&\Rightarrow S_{\overset{\triangle}{AEH}}+S_{\overset{\triangle}{BEH}}+90=2\times99\\&\Rightarrow S_{\overset{\triangle}{AEH}}+S_{\overset{\triangle}{BEH}}+90=198\\&\Rightarrow S_{\overset{\triangle}{AEH}}+S_{\overset{\triangle}{BEH}}=198-90\\&\Rightarrow S_{\overset{\triangle}{AEH}}+S_{\overset{\triangle}{BEH}}=108\\&\Rightarrow S_{\overset{\triangle}{ABH}}=108.\end{aligned}\]
پرسش. آیا می‌توانید مساحت مثلث‌های \(AEH\) و \(BEH\) را به‌دست آورید؟
با استفاده از قضیهٔ میانه-مساحت، داریم:
\[\frac{S_{\overset{\triangle}{AEH}}}{54}=\frac{S_{\overset{\triangle}{BEH}}}{135}.\]
با استفاده از قضیهٔ میانه-مساحت در مثلث \(ADE\) داریم:
\[\begin{aligned}\frac{EH}{DH}=\frac{S_{\overset{\triangle}{AEH}}}{S_{\overset{\triangle}{ADH}}}=\frac{S_{\overset{\triangle}{AEH}}}{54}.\quad(6)\end{aligned}\]
با استفاده از قضیهٔ میانه-مساحت در مثلث \(BDE\) داریم:
\[\begin{aligned}\frac{EH}{DH}=\frac{S_{\overset{\triangle}{BEH}}}{S_{\overset{\triangle}{BDH}}}=\frac{S_{\overset{\triangle}{BEH}}}{135}.\quad(7)\end{aligned}\]
از رابطه‌های \((6)\) و \((7)\) نتیجه میشود:
\[\frac{S_{\overset{\triangle}{AEH}}}{54}=\frac{S_{\overset{\triangle}{BEH}}}{135}.\]
در نتیجه:
\[\begin{aligned}&\frac{S_{\overset{\triangle}{AEH}}}{54}=\frac{S_{\overset{\triangle}{BEH}}}{135}\\[8pt]&\Rightarrow S_{\overset{\triangle}{AEH}}=\frac{54}{135}S_{\overset{\triangle}{BEH}}\\[8pt]&\Rightarrow S_{\overset{\triangle}{AEH}}=\frac{2}{5}S_{\overset{\triangle}{BEH}}.\quad(8)\end{aligned}\]
حال، از رابطه‌های \((5)\) و \((8)\) نتیجه میشود:
\[\begin{aligned}S_{\overset{\triangle}{AEH}}&=\frac{216}{7}\\[7pt]S_{\overset{\triangle}{BEH}}&=\frac{540}{7}.\end{aligned}\]
\[\begin{aligned}\left.\begin{aligned}S_{\overset{\triangle}{AEH}}+S_{\overset{\triangle}{BEH}}=108\\[8pt]S_{\overset{\triangle}{AEH}}=\frac{2}{5}S_{\overset{\triangle}{BEH}}\end{aligned}\right\}&\Rightarrow\frac{2}{5}S_{\overset{\triangle}{BEH}}+S_{\overset{\triangle}{BEH}}=108\\[8pt]&\Rightarrow\frac{7}{5}S_{\overset{\triangle}{BEH}}=108\\[8pt]&\Rightarrow S_{\overset{\triangle}{BEH}}=108\times\frac{5}{7}\\[8pt]&\Rightarrow S_{\overset{\triangle}{BEH}}=\frac{540}{7}.\end{aligned}\]
حال با جایگذاری مقدار \(S_{\overset{\triangle}{BEH}}\) در رابطهٔ \((8)\) داریم:
\[\begin{aligned}S_{\overset{\triangle}{AEH}}&=\frac{2}{5}S_{\overset{\triangle}{BEH}}\\[7pt]&=\frac{2}{5}\times\frac{540}{7}\\[7pt]&=\frac{2}{1}\times\frac{108}{7}\\[7pt]&=\frac{216}{7}.\end{aligned}\]