قضیه فیثاغورس. در هر مثلث قائمالزاویه مربع اندازهٔ وتر با مجموع مربعهای اندازهٔ دو ضلع دیگر برابر است.
عکس قضیه فیثاغورس. اگر در مثلثی مربع اندازهٔ یک ضلع با مجموع مربعهای اندازهٔ دو ضلع دیگر برابر باشد، آن مثلث قائمالزاویه است.
فرض. مثلثی، مانند \(ABC\)، یک زاویهٔ قائمه، مانند زاویهٔ \(C\)، دارد.
حکم. \(AB^2=AC^2+BC^2\).
در عکس قضیه، جای فرض و حکم عوض میشود.
اثبات قضیهٔ فیثاغورس. فرض کنیم \(ABC\) یک مثلث قائمالزاویه باشد که \(\widehat{C}=90^\circ\) و اضلاع زاویههای حادهٔ آن بهصورت زیر نامگذاری شده باشند.
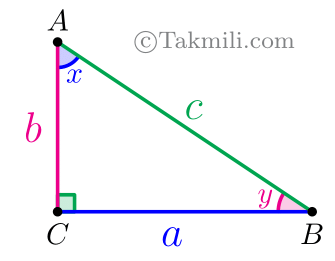
میخواهیم ثابت کنیم که \(a^2+b^2=c^2\).
مربعی به ضلع \(a+b\) رسم میکنیم و مطابق شکل زیر، هر ضلع آن را به دو قسمت با اندازههای \(a\) و \(b\) تقسیم میکنیم.
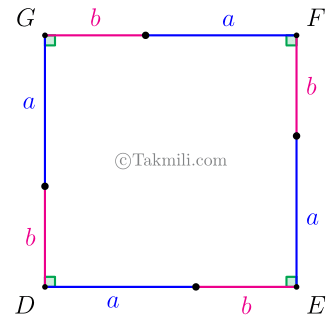
واضح است که مساحت مربع \(DEFG\) برابر است با: \[\begin{aligned}S_{DEFG}&=(a+b)^2\\&=a^2+b^2+2ab.\quad(1)\end{aligned}\]
در شکل، نقاط روی ضلعهای \(DE\)، \(EF\)، \(FG\)، و \(GD\) را بهترتیب \(M\)، \(N\)، \(P\)، و \(Q\) مینامیم. حال، اگر چهارضلعی \(MNPQ\) را رسم کنیم، چهار مثلث قائمالزاویه تشکیل میشود که بنابه حالت ضزض، هریک از آنها با مثلث \(ABC\) همنهشت است(؟). در نتیجه، اندازهٔ وتر هریک از این مثلثهای قائمالزاویه برابر \(c\) است و اندازهٔ زاویههای حادهٔ آنها بهصورت زیر است.
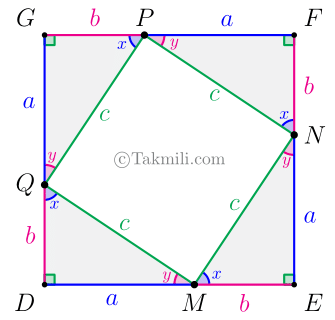
اکنون بهسادگی میتوان نشان داد که چهارضلعی \(MNPQ\) مربع است. (چگونه؟)
پس مساحت مربع \(DEFG\) از مجموع مساحت چهار مثلث قائمالزاویهٔ همنهشت و یک مربع به ضلع \(c\) نیز بهدست میآید: \[\begin{aligned}S_{DEFG}&=4\Big(\frac{1}{2}ab\Big)+c^2\\[7pt]&=2ab+c^2.\quad(2)\end{aligned}\]
از رابطههای \((1)\) و \((2)\) نتیجه میشود:
\[\begin{aligned}&a^2+b^2+2ab=2ab+c^2\\&\Rightarrow a^2+b^2=c^2.\end{aligned}\]
اثبات عکس قضیهٔ فیثاغورس. فرض کنید در مثلث \(ABC\) داشته باشیم، \(AB^2+AC^2=BC^2\). میخواهیم ثابت کنیم که \(\widehat{A}=90^\circ\).
یک زاویهٔ قائمه رسم میکنیم و آن را \(\widehat{A’}\) مینامیم. روی ضلعهای این زاویه، نقاط \(B’\) و \(C’\) را طوری انتخاب میکنیم که \(A’B’=AB\) و \(A’C’=AC\).
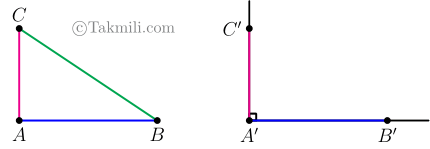
در اینصورت \[BC=B’C’.\quad(1)\] (چرا؟)
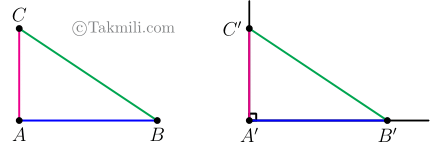
در نتیجه، دو مثلث \(ABC\) و \(A’B’C’\) در حالت ضضض همنهشت هستند. (چرا؟)
از همنهشتی دو مثلث \(ABC\) و \(A’B’C’\) نتیجه میشود: \[\widehat{A}=\widehat{A^\prime}=90^\circ.\]




سلام.
نمیشه مثلث دوم در عکس قضیه فیثاغورس رو از ضلع AB یا AC مثلث اول تقارن بدیم؟
منظورم اینه که این طوری از اثبات همنهشتی دو مثلث تقارن یافته، میشه نتیجه گرفت که چون زاویه A1 و A2 مجموعشون 180 درجه ست و چون زاویه A1 و A2 با هم برابرند، پس اندازشون 90 درجه هستش.
سلام
در راهحل شما، چرا مجموع زاویههای \(A_1\) و \(A_2\) برابر \(180\) درجه است؟
ببخشید در اثبات عمس قضیه فیثاغورس چطوری از هم نهشتی دو مثلث میشه فهمدی که Â=Á=90
توجه کنید که در ابتدای راهحل، زاویهٔ \(A^{\prime}\) را خودمان قائمه رسم کردیم.
عالی بود
سلام میشه با برهان خلف اثباتش کرد؟
اگر اثبات میشه لطف کنید این مطلب رو هم اضافه کنید
سلام
برای مطالعهٔ همهٔ اثباتهای متفاوت قضیهٔ فیثاغورس، اینجا را کلیک کنید.
می شه لطفا بگید از کجا به این می فهمیم که ۲ab=c²؟ (اثبات اول)
من هرچه گشتم ندیدم جایی نوشته باشیم \(2ab=c^2\). و اصلاً \(2ab\) با \(c^2\) برابر نیست!
ببخشید منظورم a² + b² = c² بود.
در رابطههای \((1)\) و \((2)\) مساحت مستطیل \(DEFG\) را بهصورت دو عبارت جبری متفاوت، بهدست آوردهایم. در انتهای راهحل، این دو عبارت جبری را برابر هم قرار دادهایم و با حذف \(2ab\) از طرفین تساوی، به \(a^2+b^2=c^2\) رسیدهایم.
این قضیرو هم میشه با روابط بین کسینوس ها هم اثبات کرد
منظورتان با استفاده از قضیهٔ کسینوسهاست؟ آیا در اثبات قضیهٔ کسینوسها از قضیهٔ فیثاغورس استفاده نمیکنید؟
سلام
ببخشید یک سوال داشتم. وقتی ما مثلا قضیه P را اثبات می کنیم هنگام اثبات عکس قضیه P می توانیم در اثباتمان از خود P استفاده کنیم؟
باتشکر
سلام
بله! میتوانیم.
به نظر من نمیشه از قضیه برای عکسش استفاده کرد . در این صورت نصف سوالات اثباتی از بین می رفت .
احتمالاً شما مفهوم قضیه و عکس آن را بهخوبی درک نکردهاید.
در اثبات قضیهها نباید دور ایجاد شود. مثلاً نمیتوان در اثبات قضیهٔ مجموع زاویههای مثلث از قضیهٔ زاویهٔ خارجی استفاده کرد و همزمان در اثبات قضیهٔ زاویهٔ خارجی هم از قضیهٔ مجموع زاویههای مثلث استفاده کرد!
در اثبات قضیه فیثاغورس و عکس آن دور ایجاد نمیشود.
وقتی هنوز قضیه فیثاغورس برای ما اثبات نشده است با چه منظقی میتوان از آن برای اثبات چیزی استفاده کرد ؟ وقتی این اثبات ارزشمند است که با پایه ی ریاضیات اثبات شود ، نه با قضیه ای که هنوز در مسعله اثبات نشده است
متوجه منظور شما نشدم!
در نوشتهٔ بالا که اثبات قضیهٔ فیثاغورس هست و مشکلی هم ندارد.
سلام
ببخشید معنی مربع سیاه در استدلال های هندسی چیست؟
سلام
آیا در نوشتهٔ بالا از «مربع سیاه» استفاده شده است؟
لطفاً سؤالتان را کمی دقیقتر یا با یک مثال تشریح کنید.
اشتباه شد ببخشید
میشه لطفا قضیه فیثاغورس و عکسشو به صورت یه قضیه ی دو شرطی بنویسین؟
در یک مثلث، یک زاویه قائمه است اگر و تنها اگر مربع یک ضلع برابر مجموع مربعات دو ضلع دیگر باشد.
سلام ببخشید شما توی این خط(هر یک از ان ها با مثلث ABC همنهشت است (؟)) جلوی است علامت سوال گذاشتین اون برای چیه؟
برای اینکه خواننده خودش فکر کند و دو ضلع و زاویهٔ بینِ برابر را پیدا کند.
عالییییییبیییییی
نه اینطور نیست
بسیار عالی
عالي?????????