مطالب تدریس شده در کلاس
- زیبا از مبدأ مختصات (نقطهٔ \(\big[{0\atop0}\big]\)) شروع به حرکت میکند. او در هر گام میتواند یک واحد به بالا، پایین، چپ، یا راست حرکت کند، اما نمیتواند در یک ردیف دو بار پشت سر هم حرکت کند. برای مثال، او نمیتواند از \(\big[{0\atop0}\big]\) به \(\big[{1\atop0}\big]\) و بعد به \(\big[{2\atop0}\big]\) برود. کمترین تعداد حرکتی که او میتواند برای رسیدن به نقطۀ \(\big[{1056\atop1007}\big]\) انجام دهد، چند حرکت است؟
- عدد طبیعی \(n\)، \(8\)تا شمارنده دارد. دوتا از این شمارندهها \(14\) و \(21\) هستند. حاصلجمع همهٔ شمارندههای \(n\) را بیابید.
- از هریک از انواع ششتا ۴حجرهای بالا، دو تا داریم. با این ۴حجرهایها تعدادی مکعب توپُر $2\times 2\times 2$ ساختهایم. چند نوع از این ۴حجرهایها امکان ندارد در این مکعبهای ساخته شده بهکار رفته باشد؟
- شکل زیر، یک ۳حجرهای است. سه نقطهٔ \(A\)، \(B\)، و \(C\) از یک سطح مقطع داده شده است. کدامیک از نقطههای زیر روی این سطح مقطع قرار ندارد؟
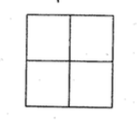
- شکل زیر، نمای بالا و روبهروی یک چندحجرهای را نشان میدهد. حجم این چندحجرهای حداقل چقدر است؟
- علی خانههای یک جدول \(3\times3\) را همانند شکل زیر، سیاه و سفید کرده است. حسین بدون اینکه از رنگآمیزی علی اطلاعی داشته باشد، یکی از خانههای جدول را انتخاب میکند. سپس، علی رنگ این خانه را تغییر میدهد (از سیاه به سفید و برعکس). احتمال اینکه در جدول حاصل سطر یا ستونی وجود داشته که هر سه خانهٔ آن همرنگ باشند چقدر است؟

- در کلاه یک شعبدهباز $9$ موش و تعدادی خرگوش وجود دارد. اگر احتمال بیرون آوردن یک خرگوش از این کلاه $\frac{4}{7}$ باشد، تعداد خرگوشها چقدر است؟
- در کلاه یک شعبدهباز $n$ موش و تعدادی خرگوش وجود دارد. اگر بدانیم \(n\) عددی کوچکتر از \(13\) و احتمال بیرون آوردن یک خرگوش از این کلاه $\frac{4}{7}$ باشد، تعداد خرگوشها چندتا میتواند باشد؟
- چهار جفت جوراب در یک کیسه وجود دارد. دو لنگه به تصادف از این کیسه بیرون میکشیم. احتمال اینکه این جورابها لنگه به لنگه باشند، چقدر است؟
- ده نفر را بهتصادف در یک صف قرار دادهایم. علی و محسن دو نفر از این ده نفر هستند. چقدر احتمال دارد که در این صف، علی جلوتر از محسن ایستاده باشد؟ (لزومی ندارد که علی و محسن پشت سر هم باشند.)
- مطابق مراحل زیر، میتوان به هر پارهخط یک دستانداز اضافه کرد:
- شکل زیر، گستردهٔ یک مکعب را نشان میدهد که روی وجههای آن اعداد \(1\) تا \(6\) نوشته شده است.
باتوجهبه متن زیر، به سه سؤال بعد از آن پاسخ دهید.
به جسمهای سهبعدی که از بههم چسباندن یک (یا چند) وجهِ مکعبهای واحد به یکدیگر ساخته میشوند، «چندحجرهای» میگوییم. برای مثال، در زیر، شش نوع ۴حجرهای را مشاهده میکنید.

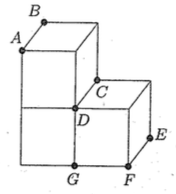
۱) \(D\)
۲) \(E\)
۳) \(F\)
۴) \(G\)
مرحلهٔ اول. پارهخط را به سه قسمت مساوی تقسیم میکنیم.
مرحلهٔ دوم. یک مثلث متساویالاضلاع روی پارهخط میانی میسازیم.
مرحلهٔ سوم. پارهخط میانی را حذف میکنیم.
در شکل زیر، سه مرحلهٔ بالا روی پارهخطی به طول \(3\) اجرا شده است.

الف) پارهخطی به طول \(21\) داریم. بعد از اینکه یک دستانداز روی آن ایجاد کنیم، طول پارهخط چقدر میشود؟
ب) روی یک پارهخط یک دستانداز ایجاد کردهایم و طول آن \(210\) شده است. طول پارهخط اولیه چقدر بوده است؟
ج) مونا روی پارهخطی به طول \(36\) یک دستانداز ایجاد کرد و آن را مسیر ۱ نامید. سپس روی هریک از پارهخطهای مسیر ۱، یک دستانداز ساخت تا مسیر ۲ ساخته شود. بعد، همین عملیات را روی مسیر ۲ انجام داد تا مسیر ۳ ساخته شود. طول مسیر ۳ چقدر است؟
در شکل زیر، مسیر ۱ و مسیر ۲ مونا رسم شده است.
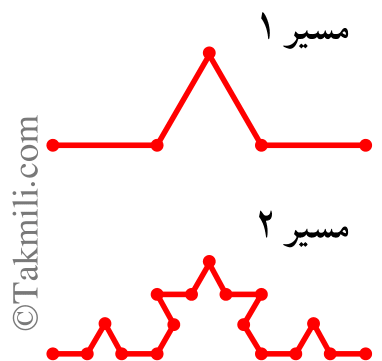
د) آرمیتا روی یک پارهخط به طول \(n\) یک دستانداز ایجاد کرد و مسیر ساخته شده را مسیر ۱ نامید. سپس روی هریک از پارهخطهای مسیر ۱ یک دستانداز ایجاد کرد و مسیر ساخته شده را مسیر ۲ نامید. او همین کار را تکرار کرد تا مسیر ۳، مسیر ۴، و مسیر ۵ ساخته شوند. اگر \(n\) عددی طبیعی بوده باشد و طول مسیر ۵ نیز عددی طبیعی شود، آنوقت کمترین مقدار ممکن برای \(n\) چیست؟

فرض کنید تعداد زیادی از مکعبهای بالا داشته باشیم. اگر تعدادی از آنها را بهصورت زیر، به یکدیگر بچسبانیم و شکل حاصل را بهصورت زیر، روی یک میز قرار دهیم، مجموع عددهای نوشته شده روی وجههایی که دیده میشوند، حداکثر چقدر است؟

تمرینهای روزانه
بهزودی!





