نهم. فصل ۳. قضیهٔ فیثاغورس و عکس آن
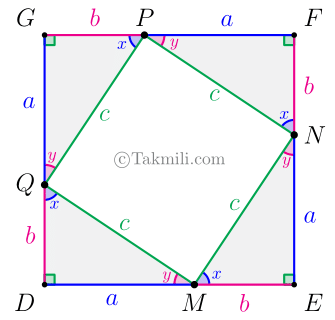
قضیه فیثاغورس. در هر مثلث قائمالزاویه مربع اندازهٔ وتر با مجموع مربعهای اندازهٔ دو ضلع دیگر برابر است. عکس قضیه فیثاغورس. اگر در مثلثی مربع اندازهٔ یک ضلع با مجموع مربعهای اندازهٔ دو ضلع دیگر برابر باشد، آن مثلث قائمالزاویه است. فرض. مثلثی، مانند \(ABC\)، یک زاویهٔ قائمه، مانند زاویهٔ \(C\)، دارد. حکم. \(AB^2=AC^2+BC^2\). در […]
نهم. فصل ۳. قضیهٔ وتر و یک ضلع
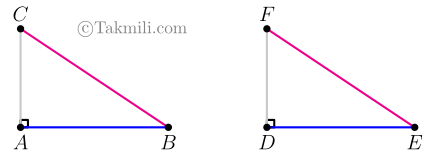
قضیهٔ وتر و یکضلع. اگر وتر و یک ضلع از یک مثلث قائمالزاویه با اجزاء نظیر از مثلث قائمالزاویهای دیگر برابر باشند، آنگاه این دو مثلث همنهشتاند. فرض. وتر و یک ضلع از یک مثلث، مانند \(ABC\)، با اجزاء نظیر از مثلثی دیگر، مانند \(DEF\) برابر است. حکم. دو مثلث \(ABC\) و \(DEF\) همنهشت هستند. […]
نهم. فصل ۳. قضیهٔ نیمساز و عکس آن

قضیه نیمساز. هر نقطه روی نیمساز یک زاویه از دو ضلع آن زاویه فاصلهٔ یکسان دارد. عکس قضیه نیمساز. اگر نقطهای از دو ضلع یک زاویه فاصلهٔ یکسان داشته باشد، این نقطه روی نیمساز آن زاویه قرار دارد. فرض. نقطهای مانند \(D\) روی نیمساز زاویهای مانند \(A\) قرار دارد. حکم. فاصلهٔ نقطهٔ \(D\) از دو […]
نهم. فصل ۳. قضیهٔ شعاع و مماس
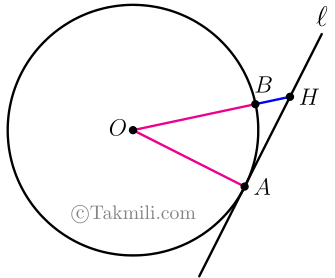
قضیهٔ شعاع و مماس. شعاع دایره در نقطه تماس بر خط مماس عمود است. فرض. خطی مانند \(\ell\) بر دایرهای مماس است. حکم. خط \(\ell\) بر شعاعی که از محل برخورد \(\ell\) با دایره میگذرد، عمود است. اثبات. فرض کنیم خط \(\ell\) بر دایرهای به مرکز \(O\) مماس باشد. نقطهٔ تماس را \(A\) مینامیم. میخواهیم […]
نهم. فصل ۳. قضیهٔ کمان و وتر

قضیه کمان و وتر. وترهای نظیر دو کمان برابر، برابرند و برعکس. فرض. در یک دایره دو وتر، مانند \(AB\) و \(CD\) برابرند. حکم. در این دایره، کمانهای \(AB\) و \(CD\) برابرند. در عکس قضیه، جای فرض و حکم عوض میشود. اثبات قضیه کمان و وتر. دایرهای به مرکز \(O\) را در نظر بگیرید. فرض […]
نهم. فصل ۳. قضیهٔ زاویهٔ محاطی

قضیهٔ زاویهٔ محاطی. اندازهٔ هر زاویهٔ محاطی با نصف کمان روبهرو به آن زاویه برابر است. فرض. زاویهای، مانند زاویهٔ \(ABC\)، یک زاویهٔ محاطی در یک دایره است. حکم. اندازهٔ زاویهٔ \(ABC\)، نصف اندازهٔ کمان \(AC\) است. اثبات. فرض کنیم نقطهٔ \(O\) مرکز دایره باشد. سهحالت برای زاویهٔ \(ABC\) در نظر میگیریم: حالت اول. نقطهٔ […]