اصل ضزض (دو ضلع و زاویه بین). اگر دو ضلع و زاویهٔ بین آنها از مثلثی با دو ضلع و زاویهٔ بین آنها از مثلثی دیگر برابر باشند، آنگاه این دو مثلث همنهشتاند.
فرض. دو ضلع و زاویهٔ بین آنها از مثلثی با دو ضلع و زاویهٔ بین آنها از مثلثی دیگر برابر هستند.
حکم. این دو مثلث همنهشتاند.
ماروین جی گرینبرگ در (صفحهٔ ۹۳ و ۹۴) کتاب هندسههای اقلیدسی و نااقلیدسی دربارهٔ اصل ضزض، اینگونه نوشته است:
همانگونه که گفتیم، اقلیدس ضزض را یک اصل نگرفته، بلکه سعی کرده است آن را بهعنوان قضیهای ثابت کند. برهای وی اینچنین است.
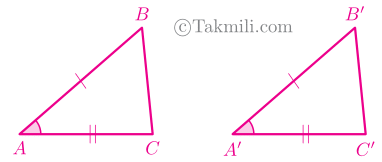
مثلث \(A’B’C’\) را چنان حرکت میدهیم که \(A’\) روی \(A\) قرار گیرد و \(A’B’\) بر \(AB\). از آنجا که مطابق فرض \(AB=A’B’\)، پس \(B’\) باید بر نقطهٔ \(B\) منطبق شود. چون \(\widehat{A}=\widehat{A’}\)، \(A’C’\) باید بر \(AC\) قرار گیرد، و چون \(AC=A’C’\)، نقطهٔ \(C’\) باید بر \(C\) منطبق شود. لذا \(B’C’\) بر \(BC\)، و بقیهٔ زاویهها بر بقیهٔ زاویهها منطبق خواهند شد، و بدینترتیب مثلثها همنهشت میشوند.
این برهان برهمنهش نام دارد و از تجربه رسم دو مثلث بر یک صفحهٔ کاغذ و بریدن یکی از آنها و گذاشتن به روی دیگری ناشی شده است. اگرچه این راه برای متقاعد کردن یک مبتدی هندسه در قبول ضزض راه خوبی است، ولی این، برهان نیست. اقلیدس آن را با اکراه، جز در اینجا، تنها در یک جای دیگر هم بهکار برده است. این یک برهان نیست زیرا اقلیدس هرگز اصلی ذکر نکرده که به اتکای آن شکلها بتوانند حرکت کنند بیآنکه اندازه و شکلشان تغییر کند.
برخی از مؤلفان جدید «حرکت» را اصطلاحی تعریف نشده میگیرند و اصولی برای این اصطلاح وضع میکنند. (برای مثال، در «مبانی هندسه» اثر پیری، «نقطه» و «حرکت» تنها اصطلاحات تعریف نشدهاند.) و در غیر اینصورت هندسه برمبنای دیگری بنا میشود، یعنی «فاصلهها» مطرح میشوند و «حرکت» بهعنوان تبدیل یکبهیک صفحه بر روی خودش، که فاصله را حفظ میکند، تعریف میشود. احکام هندسه اقلیدس را میتوان با هر دو روش اثبات کرد. در واقع فلیکس کلاین در برنامهٔ ارلانگر خود در \(1872\)، هندسه را مطالعهٔ ویژگیهایی از شکلها تعریف میکند که بر اثر گروه خاصی از تبدیلات، ناوردا میمانند.


من یه سوال داشتم الان ما مگه نمیگیم این اصل فلانه و اصل یعنی اینکه اولیه است و استدلالی بر آن وجود ندارد پس چطوری اثبات برش مینویسیم مگه اولیه نیس ما اون رو بدون استدلال قبول میکنیم
برای «اصل» اثبات نمینویسیم. درستیِ «اصل» را بدون اثبات میپذیریم.
آیا با حالت دو ضلع و زاویه ی غیر بین می توان گفت دو مثلث هم نهشت اند ؟ اگه نه چرا ؟
خیر.
در تمرینهای ۱۲ و ۱۳ صفحههای ۹۸ و ۹۹ کتاب ریاضی تکمیلی هشتم، بهطور کامل به این موضوع پرداخته شده است.
دانلود رایگان کتابهای ریاضی تکمیلی
یا مثلا وقتی میگیم در متوازی الاضلاع ضلع های روبرو موازی هستن خب این تعریف متوازی الاضلاع هست و باید به عنوان یه موضوع بپذیریم اون رو ( مثل اصل ) پس می تونیم بگیم اصل هست ؟
خیر! در تعریف، یک موجود را معرفی میکنیم. و برای اینکه دقیقاً مشخص باشد که آن موجود چیست، ویژگیهایی از آن موجود را ذکر میکنیم.
سلام ! یه سوال داشتم آیا تعاریف همون اصل ها هستن ؟ مثلا میگیم مربع متوازی الاضلاعی هست که چهار ضلعش برابره الان این رو به عنوان یه اصل میتونیم در نظر بگیریم ؟
سلام
خیر! در ریاضیات «تعریف» و «اصل» دو موجود متفاوت هستند.
سلام
الان ایراد این اثبات این هست که ما نمیدونیم که حرکت اندازه ضلع / زاویه رو تغییر بده یا نه درسته؟
سلام
خیر! باید برای «حرکت» تعریف دقیق ریاضیاتی ارائه داد تا بتوان از آن استفاده کرد.
سلام ببخشید این که یک اصله دیگه فرض و حکم نداره که چون استدلالی براش نیست درسته؟
پس چرا سوال گفته فرض و حکم رو بنویس یا فقط برای قضیه هاست؟
سلام
فرض و حکم ربطی به اصول و غیر اصول ندارد!
فرض، «دادهٔ» یک گزاره (جمله) ریاضی است و حکم، «خواستهٔ» آن گزاره.
در اصول، درستیِ خواستهٔ گزاره، بدون اثبات پذیرفته میشود.
اصل قوی تره یا قضیه؟؟
لطفاً بگید «قویتر» بودن در ریاضیات یعنی چه؟
«اصل» عبارتی است که درستی آن را بدون استدلال میپذیریم.
«قضیه» عبارتی است که درستی آن را با حقایقی که قبلاً پذیرفتهایم، اثبات میکنیم.
بههرحال، این دو از یک جنس نیستند که بخواهید آنها را مقایسه کنید.
ببخشید تفاوت اصل با قضیه چیه؟
اصل، عبارتی است که بدون دلیل آن را میپذیریم. اما قضیه عبارتی است که با استفاده از اصلها و تعاریف درستی آن را ثابت میکنیم.