قضیهٔ ززض. اگر دو زاویه و ضلع غیر بین آنها از یک مثلث با دو زاویه و ضلع غیر بین آنها از مثلثی دیگر، نظیر به نظیر برابر باشند، آنگاه این دو مثلث همنهشتاند.
فرض. دو زاویه و ضلع غیربین آنها از یک مثلث با اجزاء نظیر از مثلثی دیگر برابر است.
حکم. این دو مثلث همنهشت هستند.
اثبات. فرض کنیم در مثلثهای \(ABC\) و \(A’B’C’\) داشته باشیم \(\widehat{A}=\widehat{A’}\)، \(\widehat{B}=\widehat{B’}\)، و \(AC=A’C’\).

پس بنابه قضیهٔ مجموع زاویههای مثلث داریم:
\[\left.\begin{aligned}&\widehat{A}+\widehat{B}+\widehat{C}=180^\circ\\&\widehat{A’}+\widehat{B’}+\widehat{C’}=180^\circ\\&\widehat{A}=\widehat{A’}\\&\widehat{B}=\widehat{B’}\end{aligned}\right\}\Rightarrow\widehat{C}=\widehat{C’}.\]
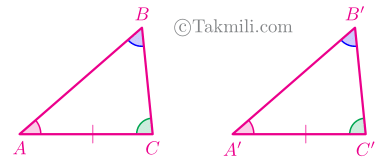
حال، چون یک ضلع از مثلث اول با ضلع نظیرش در مثلث دوم برابر است، پس این دو مثلث بنابه حالت زضز همنهشت هستند.
وتر و یک زاویهٔ تند، و قضیهٔ ززض
«وتر و یک زاویهٔ تند» مسخرهترین قضیه در کتابهای درسی است!
«وتر و یک زاویهٔ تند» میگوید:
در دو مثلث قائمالزاویه، واضح است که زاویههای قائمه برابرند. اگر وتر و یک زاویهٔ تند یکی از این مثلثها با وتر و یک زاویهٔ تند مثلث دیگر برابر باشد، آنوقت این دو مثلث همنهشت هستند.
در واقع، در دو مثلث فرض شده در «وتر و یک زاویهٔ تند»، دو زاویه (زاویهٔ قائمه و یک زاویهٔ تند) و ضلع غیر بین آنها (وتر) از یک مثلث با اجزاء نظیر از مثلث دیگر، برابرند.
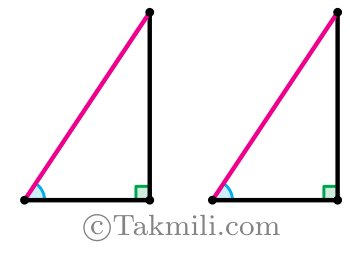
آیا چنین خاصیتی فقط در مثلثهای قائمالزاویه برقرار است؟! یعنی اگر در دو مثلث دلخواه، دو زاویه و ضلع غیر بین یکی از مثلثها با اجزاء نظیر آنها در مثلث دیگر برابر باشد، آن دو مثلث همنهشت نیستند؟!!
یکی از قضیههای مهم در همنهشتی مثلثها، قضیهٔ ززض است.
قضیهٔ ززض میگوید:
اگر دو زاویه و ضلع غیر بین آنها از یک مثلث با دو زاویه و ضلع غیر بین آنها از مثلثی دیگر، نظیر به نظیر برابر باشند، آنگاه این دو مثلث همنهشتاند.
وقتی قضیهٔ ززض برای همهٔ مثلثها برقرار است و اثبات آن نیز بسیار ساده است، چرا باید خودمان را به مثلثهای قائمالزاویه محدود کنیم و این قضیه را در حالت خاص، وتر و یک زاویهٔ تند بنامیم؟!
قضیهٔ ززض در اکثر کتابهای درسی نیست. و توجه کنید که فقط در این قضیه است که باید نظیر به نظیر بودن ضلعها و زاویهها، دقیقاً بررسی شود. اگر کسی مفهوم ضلعها و زاویههای متناظر را نداند، نمیتواند بهدرستی از قضیهٔ ززض استفاده کند. بنابراین، به معلمان و دانشآموزان اکیداً توصیه میشود که این قضیه را بیاموزند و از آن در تمرینها استفاده کنند. در ادامه، تمرینهایی از کتابهای ریاضی تکمیلی آمدهاند که به درک بهتر قضیهٔ ززض کمک میکنند.
تمرین ۱۱ صفحهٔ ۹۸ کتاب ریاضی تکمیلی هشتم. با ذکر دلیل مشخص کنید که کدامیک از عبارتهای زیر همواره درست است و کدامیک همواره درست نیست.
الف) اگر دو زاویه و یک ضلع مثلثی با دو زاویه و یک ضلع از مثلث دیگر برابر باشند، آن دو مثلث همنهشتاند.
ب) اگر دو زاویه و یک ضلع از مثلثی با دو زاویه و یک ضلع از مثلث دیگر نظیر به نظیر برابر باشند، آن دو مثلث همنهشتاند.
تمرین ۴ صفحهٔ ۵۱ کتاب ریاضی تکمیلی نهم. چرا در قضیهٔ «ززض»، از عبارت «نظیر به نظیر» استفاده شده ولی در قضیهٔ «زضز» از عبارت «نظیر به نظیر» استفاده نشده است؟


ارسال کامنت و دیدگاه
در اولین فرصت به کامنت شما پاسخ میدهیم و بلافاصله یک ایمیل برایتان ارسال میکنیم. ❤️ببخشید راجب قضیه دو زاویه و ضلع بین استاد ما گفتن که هر حالت همنهشتی نیازی به حالت دیگری ندارد
اینجا برای اثبات قضیه دو زاویه و ضلع غیر بین از حالت دو زاویه و ضلع بین استفاده شده
خودت به تنهایی خود و بدون کمک از حالت همنهشتی دیگر قابل اثبات نیست.
ایا شکل دیگری از اثبات برای این موضوع وجود داره؟
ممنون میشم راهنمایی کنید
ایشان گفتهاند «هر حالت همنهشتی نیازی به حالت دیگری ندارد» یا اینکه در هر حالت همنهشتی نباید از حالت دیگری استفاده کرد؟
اینکه حالتهای همنهشتی حتماً باید از همدیگر مستقل باشند، حرف عجیب و بیربطی است. اگر میخواهید اثباتهای هندسی را بهطور اصولی و دقیق یاد بگیرید، باید کتاب «هندسههای اقلیدسی و نااقلیدسی و بسط آنها» را بخوانید.
اثبات وتر و زاویه تند به چه صورت هستش؟
ارتباط «وتر و یک زاویهٔ تند» با قضیهٔ «ززض» به انتهای همین نوشته اضافه شد.
سلام ، وقتتون بخیر .
اثبات این قضیه بدون 5 اصل اقلیدس چگونه هستش؟
ممنون
سلام
در اثبات این قضیه بدون اصل ۵ اقلیدس از «برهان خلف» استفاده میشود که جزء مباحث ریاضی و ریاضی تکمیلی دورهٔ اول دبیرستان نیست.
این اثبات در کتاب هندسههای اقلیدسی و نااقلیدسی و بسط آنها موجود است.
سلام وقت بخیر این قضیه با برهان خلف اثباتش چجوری هست ؟
سلام
اثباتی که شما میخواهید در کتاب هندسههای اقلیدسی و نااقلیدسی هست.
منظور از نظیر به نظیر چیه تو قضیه لطف توضیح بدین
در همنهشتی دو چندضلعی، به ضلعها و زاویههای دو چندضلعی که دوبهدو باهم برابرند، «متناظر» یا «نظیر» یکدیگر میگویند.
البته این حالت یه مثال نقض هم داره که احتمال این که در این حالت پیش بیاد خیلی کمه.
لطفاً مثال نقض را بنویسید یا از آن عکس بگیرید و آپلود کنید.
در بخش کامنتگذاری پرسشهای متداول، روش آپلود عکس در سایت تکمیلی شرح داده شده است.
این دو مثلث متشابه هستند اما همنهشت نیستند.
اگر صورت قضیهٔ ززض اینگونه بود، آنوقت مثال شما یک مثال نقض بود:
اما صورت قضیهٔ ززض اینگونه است:
به اصطلاح «نظیر به نظیر» دقت کنید. در مثال شما ضلع ۵ سانتیمتری نظیر یکدیگر نیستند. (باید هر دو ضلع مقابلِ زاویههایی با اندازههای برابر باشند تا نظیر هم باشند.)
بله،منظور من هم همین بود که باید حتما در این حالت نظیر به نظیر ذکر بشود که در توضیح شما گفته شده.اما اگر سوال اطلاعات زیادی نداده باشد نمیتوانیم از این حالت استفاده کنیم درست هست؟(یعنی از نظیر به نظیر بودن اطلاعی نداشته باشیم)
در ریاضیات وقتی میتوانید از یک قضیه استفاده کنید که همهٔ شرطهای آن برقرار باشد.
بسیار متشکرم
چرا در آخر گفتيد بنا به حالت زض ز ؟
چون \(\widehat{A}=\widehat{A}^\prime\)، \(\widehat{C}=\widehat{C}^\prime\)، و \(AC=A^\prime C^\prime\).
پس چرا عنوانش اثبات ززض هست؟اين طوري ميشه دو زاويه و ضلع غير بين.اما در قسمت آخرش گفتيد زض ز که ميشه دو زاويه و ضلع بين…يعني به هر دو حالت ميشه؟
در نوشتهٔ بالا، برای اثبات قضیهٔ ززض (دو زاویه و ضلع غیر بین) از قضیهٔ زضز (دو زاویه و ضلع بین) استفاده شده است.
استاد ما گفتن که نمیشه برای اثبات یک همنهشتی از یک حالت دیگه کمک گرفت
همچنین همنهشتی ها نیازی به حالت های دیگه ندارن.
استاد شما با چه دلیلی چنین حرفی زدهاند؟
اگر میخواهید استدلالهای هندسی را بهصورت خیلی دقیق یاد بگیرید، کتاب «هندسههای اقلیدسی و نااقلیدسی و بسط آنها» را مطالعه کنید.
سلام حالت دو ضلع و زاویه ی غیر بین هم می تونن با هم همنشت باشن.
سلام
دو ضلع و زاویهٔ غیربین، حالت همنهشتی دو مثلث نیست. در صفحههای ۹۸ و ۹۹ کتاب ریاضیات تکمیلی هشتم، بهطور مفصل دراینباره بحث شده است.
عالی