مسئلهٔ \(3n+1\) یا حدس کولاتز یکی از مسائل حل نشدهٔ ریاضیات است. صورت این مسئله بسیار ساده است بهطوریکه یک دانشآموز کلاس چهارمی بهراحتی آن را متوجه میشود. اما ریاضیدانان بسیاری نتوانستهاند آن را حل کنند.
پال اردوش، ریاضیدان مشهور قرن بیستم گفته است: «ریاضیات زمان ما این آمادگی را ندارد که با چنین هیولایی در بیوفتد!»
صورت مسئلهٔ \(3n+1\) در کتابهای زیادی، از جمله کتاب ریاضیات تکمیلی هشتم شرح داده شده است:

سدریک ویلانی، برندهٔ مدال فیلدز و نویسندهٔ کتاب تولد یک قضیه، دربارهٔ حدس کولاتز گفته است: «هر کس بتواند این حدس را اثبات یا نقض کند مانند یک قهرمان از او استقبال خواهد شد. من که مسلماً امتحان نخواهم کرد: علاوه بر اینکه مسئلهای است فوقالعاده غامض، با روحیهٔ من هم سازگاری ندارد. مغز من برای تفکر در این سبک از مسائل تعلیم ندیده است.»
ویدئوی اول
در ویدئوی زیر، علاوه بر توضیحاتی دربارهٔ صورت مسئله، دنبالههایی مربوط به آن نیز معرفی میشوند.
در ویدئوی بالا، یک درخت بزرگ و چند دنباله از سایت oeis.org نشان داده میشود.
درخت بزرگ!
برای مشاهدهٔ درختی که در ویدئوی بالا نمایش داده شد، اینجا را کلیک کنید.
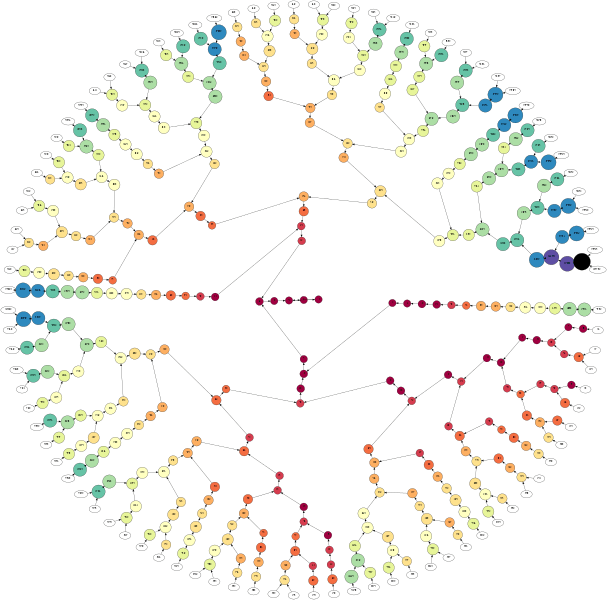
در صفحهٔ مربوط به حدس کولاتز سایت ویکپدیا، درختها و نمودارهای بزرگ و جالبی وجود دارد. برای نمونه، شکل زیر را ببینید.
دنبالهٔ A177729
اگر در فرایند گفته شده در حدس کولاتز از عددی مانند \(n\) شروع کنیم و به \(1\) برسیم، یک دنباله از اعداد طبیعی ساخته میشود که به آن دنبالهٔ کولاتزِ عدد \(n\) میگوییم.
در زیر، دنبالهٔ کولاتز اعداد \(1\) تا \(6\) آمده است.
\[\begin{aligned}&{\color{purple}1}.\\&{\color{purple}2},1.\\&{\color{purple}3},10,5,16,8,4,2,1.\\&{\color{purple}4},2,1.\\&{\color{purple}5},16,8,4,2,1.\\&{\color{purple}6},3,10,5,16,8,4,1.\end{aligned}\] عدد \(4\) و \(5\) در دنبالهٔ کولاتز عدد \(3\) آمدهاند. ولی عدد \(6\) در دنبالهٔ کولاتز اعداد کوچکتر از خود نیامده است.
دنبالهٔ A177729 شامل اعدادی است که در دنبالهٔ کولاتز اعداد کوچکتر از خود نیامده باشند:
\[1, 2, 3, 6, 7, 9, 12, 15, 18, 19, 21, 24, 25, 27, 30,\dots.\]
پرسش ۱. به نظر شما، آیا شناخت کامل دنبالهٔ A177729 میتواند به حل مسئلهٔ \(3n+1\) کمک میکند؟
دنبالهٔ A060412
میخواهیم لیستی از اعداد طبیعی بسازیم. قانون اضافه کردن اعداد طبیعی به این لیست را با چند مثال شرح میدهیم.
1. در دنبالهٔ کولاتزِ عدد \(1\)، هیچوقت به عددی کوچکتر از \(1\) نمیرسیم! پس قرار میدهیم \(\ell_1=0\)، و عدد \(1\) را داخل لیستمان قرار نمیدهیم.
2. در دنبالهٔ کولاتزِ عدد \(2\)، پس از \({\color{red}1}\) مرحله به عددی کوچکتر از \(2\) میرسیم: \[{\color{purple}2}, 1.\] پس قرار میدهیم \(\ell_2=1\)، و عدد \(2\) را بهعنوان اولین عدد در یک لیست مینویسیم:
\[\color{green}[2]\]
3. در دنبالهٔ کولاتزِ عدد \(3\)، پس از \(\color{red}6\) مرحله به عددی کوچکتر از \(3\) میرسیم:
\[{\color{purple}3},10,5,16,8,4,2,{\color{gray}1}.\] پس قرار میدهیم \(\ell_3={\color{red}6}\)، و چون \(\ell_3 > \ell_2\)، پس عدد \(3\) را به لیستمان اضافه میکنیم:
\[\color{green}[2, 3].\]
4. در دنبالهٔ کولاتزِ عدد \(4\)، پس از \(1\) مرحله به عددی کوچکتر از \(4\) میرسیم:
\[{\color{purple}4},2,{\color{gray}1}.\] پس قرار میدهیم \(\ell_4=1\)، و چون \(\ell_4 < \ell_3\)، پس \(4\) را به لیستمان اضافه نمیکنیم.
5. در دنبالهٔ کولاتزِ عدد \(5\)، پس از \(3\) مرحله به عددی کوچکتر از \(5\) میرسیم: \[{\color{purple}5},16,8,4,{\color{gray}2},{\color{gray}1}.\] پس قرار میدهیم \(\ell_5=3\)، و چون \(\ell_5 < \ell_3\)، پس \(5\) را به لیستمان اضافه نمیکنیم.
6. در دنبالهٔ کولاتزِ عدد \(6\)، پس از \(1\) مرحله به عددی کوچکتر از \(6\) میرسیم: \[{\color{purple}6},3,{\color{gray}10},{\color{gray}\dots}.\] پس قرار میدهیم \(\ell_6=1\)، و چون \(\ell_6 < \ell_3\)، پس \(6\) را به لیستمان اضافه نمیکنیم.
7. در دنبالهٔ کولاتزِ عدد \(7\)، پس از \({\color{red}11}\) مرحله به عددی کوچکتر از \(7\) میرسیم:
\[{\color{purple}7},22,11,34,17,52,26,13,40,20,10,5,{\color{gray}16},{\color{gray}\dots}.\] پس قرار میدهیم \(\ell_7={\color{red}11}\)، و چون \(\ell_7 > \ell_3\)، پس \(7\) را به لیستمان اضافه میکنیم:
\[\color{green}[2,3,7].\]
اگر به همین ترتیب ادامه دهیم، اعداد لیستمان دنبالهٔ زیر را میسازند:
\[\color{green}2, 3, 7, 27, 703, 10087, 35655, 270271, 362343, 381727,\dots.\] دنبالهٔ بالا، همان دنبالهٔ A060412 است که در ویدئو معرفی شد.
پرسش ۲. به نظر شما، آیا شناخت کامل دنبالهٔ A060412 میتواند به حل مسئلهٔ \(3n+1\) کمک میکند؟
ماشین حساب کولاتز
با یک جستجوی ساده میتوانید وبسایتهایی را بیابید که ماشینحساب کولاتز آنلاین دارند. برای نمونه روی لینک زیر کلیک کنید.
با استفاده از ماشینحساب کولاتز بالا، میتوایند دنبالهٔ کولاتز اعداد مختلفی را مشاهده کنید و تعداد جملههای آنها را بشمارید.
ویدئوی دوم
حتماً مسائل زیادی را دیدهاید که با استفاده از رسم شکل، بهسادگی حل میشوند. در ویدئوی زیر، یک شکل جالب برای حدس کولاتز رسم میشود که نشان میدهد که چرا حل کردن این مسئله بسیار دشوار است.



اگه میخوان ثابت کنن مثال نقضی وجود نداره… از نظرم دلیل واضحه….
واضحه؟ چهجوری؟
لطفاً استدلال واضحتان را بنویسید.
اول از همه من سن کمی دارم برای همین نمیتونم خیلی پیچیده فکر کنم یا جواب بدم ولی آخه خب همون 3n+1 برای این هست که ما بتونیم عدد رو به عددی تبدیل کنیم که بتونیم بر 2 تقسیم کنیم
خب، بله.
ولی سؤال اینه که چرا همیشه به \(8\)، \(4\)، و … میرسیم.
If even n/2
If odd 3n+1
2n is odd
2n+n is odd because n is odd
Every odd +1 is even
So n/2 is (3n+1)/2
The important is even because we can make
1+A even number with 3n
In every even numbers is factor of 2
And 2÷2 is 1
So every natural number can be 1
متوجه نشدم!
یعنی این راهحل مسئلهٔ کولاتزه؟!!!
سلام اثبات رو کجا باید ثبت کنم
من نظریه ای دارم که ثابت میکنه هیچ مثال نقضی نمیتونه وجود داشته باشه
من این حدس رو تو کتاب یکی از پایه ها دیدم
۱۶ سالمه و الان دارم وارد کلاس دوازدهم میشم رشتم ریاضی هستش و مدرسه نمونه دولتیم
لطفا اطلاع بدید
سلام
میتونید وقتی وارد دانشگاه شدید، اثباتتان را برای یکی از اساتید رشتهٔ ریاضیات محض شرح دهید. اگر مشکلی نداشته باشد، اساتید شما را راهنمایی میکنند که چگونه آن را در سطح بینالمللی منتشر کنید.
تعریف جدید برای مثال نقص حدس کولاتز دارم و مایلم از نظر علمی بررسی شود
مثال نقض شما چه عددی است؟
عددی برای مثال نقص ندارم توضیحی دارم در مورد اینکه یک مثال نقص در چه صورتی میتواند در مدار کولاتز قرار بگیرد و به یک نرسد
تا وقتی که نتوانید یک مثال نقض بسازید، راهحل شما کامل نیست.
لطفاً «کوتاهترین مقاله ریاضیات» را بخوانید.
این اثبات تقریبا چیزی شبیه به استقرای ریاضی هست قرار نیست مثال نقصی ارائه شود بلکه قرار هست نشان داده شود مثال نقصی وجود ندارد
استقرای ریاضی متفاوت از آن چیزی است که شما میفرمایید.
تا وقتی مثال نقضی نساخته باشید، نمیتوانید ادعا کنید که وجود دارد. آیا کوتاهترین مقاله ریاضیات را خواندید؟
سایتتون واقعا مطالب خوبی داره، واقعا عالیه ،
فقط از نظر من یک ایراد داره سایتتون اون هم این هست که دسترسی به مطالب خیلی راحت نیست ،
حتی من که خیلی وقته با سایتتون همراهم اما بعضی اوقات نمیتوانم سریع مطالبو پیدا کنم
آیا از جدول «دسترسی سریع» که در پایین همهٔ صفحات سایت است، استفاده میکنید؟
لطفاً با جزئیات بیشتر بگویید که به دسترسی به کدام قسمتهای سایت مشکل است تا در اسرع وقت سعی کنیم که چنین مشکلاتی را برطرف کنیم.
با سپاس از همراهی شما
مثلا مسابقه های کلاسیکو و همین مطلبی که درباره حدس کولاتز گذاشتتین
لینک مسابقهها در منوی بالای سایت هست. ولی عنوانش «مسابقه» است که باید عنوان را به «پای کلاسیکو» تغییر دهیم.
دربارهٔ ویدئوها درست میفرمایید. البته، در صفحهٔ اول سایت و در قسمت «مطالب خاص برای بچههای خاص»، لینک ویدئوی هفته هست. (و همچنین، در جدول دسترسی سریع)
شاید بهتر باشد لینکی هم برای ویدئوی هفته و کتاب در منوی بالای سایت در نظر بگیریم.
ممنون از اینکه با ما در ارتباط هستنید و مشکلات را گزارش میدهید.
سلام خسته نباشید.
یه سوال.آیا می دونستید سایتتون واقعا عالیه؟
من خیلی وقت منتظر بودم تا دربارهی این مسئله مطلبی بزارید به شدت مشتاق ویدئوی دوم هستم.خیلی ممنون ازتون.
سلام
لطفاً چنین صفحاتی را برای همهٔ دوستان و معلمانتان بفرستید.
امیدوارم با انرژی مثبتی که میدهید بتوانیم هرچه سریعتر ویدئوی دوم و سوم حدس کولاتز را نیز آماده کنیم.