برای اینکه درسنامهٔ مجموعه ها را به‌خوبی بیاموزید، حتماً روی لینک زیر کلیک کنید و از روش ارائه شده در آن استفاده کنید.
چگونه درسنامه‌های سایت تکمیلی را بخوانیم؟
فهرست
۱. مقدمه
حاصل عبارت \(8\div2(2+2)\) چیست؟
افراد به پرسش بالا، پاسخ‌های متفاوتی می‌دهند:
\[\begin{aligned}&8\div2(2+2)=8\div2(4)=8\div8=1\\[5pt]&8\div2(2+2)=4(2+2)=4(4)=16\end{aligned}\]ولی همان‌طور که می‌دانید، در ریاضیات نباید چنین عبارت محاسباتی ساده‌ای، پاسخ‌های متفاوتی داشته باشد. در ویدئوی زیر، با استفاده از نرم‌افزارهای مختلف، حاصل این عبارت را محاسبه کرده‌ایم.
واضح است که همهٔ نرم‌افزارهای بالا، برای محاسبهٔ عبارت \(8\div2(2+2)\)، باید از قانون واحدی پیروی کنند. این قوانین، که ریاضیدانان آنها را تأیید کرده‌اند، در ادامه آمده است.
۲. اولویت عملگرها
برای محاسبۀ عبارتهای ریاضی، نمادها را به‌ترتیب زیر به‌کار می‌برند.
١. پرانتز
۲. توان یا جذر
۳. ضرب یا تقسیم
۴. جمع یا تفریق
اگر در یک عبارت، دو نماد ترتیب یکسانی داشته باشند (مثلاً ضرب یا تقسیم)، ابتدا نمادی را به‌کار می‌بریم که در سمت چپ قرار دارد.
باتوجه‌به قانون‌های بالا، حاصل عبارت \(8\div2(2+2)\) را به‌دست می‌آوریم:
\[\begin{aligned}&8\div2\times(2+2)\\&=8\div2\times4\\&=4\times4\\&=16.\end{aligned}\]
۳. چند مثال
حاصل هریک از عبارتهای زیر را به‌دست آورید.
الف) \(8\times9+3^2\times2\)
ب) \(8-(3-9\times2^2)\)
ج) \(3+6(11+1-4)\div8\times2\)
د) \(4^{3^2}+\big(4^3\big)^2\)
۴. بازی محاسبه
بازی‌های رایانه‌ای زیادی با موضوع محاسبه تولید شده‌اند که می‌توانند تأثیر شگرفی در تقویت توانایی محاسباتی دانش‌آموزان و حتی بزرگسالان داشته باشند. یکی از این بازی‌ها در زیر آمده است. برای مشاهدهٔ بازی‌های دیگر، به صفحهٔ بازی سایت تکمیلی بروید.
در بازی زیر، از داخل جدول، اعداد مناسب را انتخاب کنید و آنها را در جاهای خالی قرار دهید طوری که تساوی داده شده، درست باشد.
اگر مشتری سایت تکمیلی هستید، وارد حساب کاربری‌تان شوید تا رکوردهای شما در این بازی ثبت شود.
با خرید یکی از محصولات سایت تکمیلی، مشتری سایت خواهید شد و می‌توانید در بازی‌ها با سایر کاربران رقابت کنید.
۵. زنگ تفریح
۶. آزمون آنلاین و تمرینهای بیشتر
اگر در آزمون بالا نمرهٔ قابل قبولی کسب نکرده‌اید، حتماً تمرینهای اولویت عملگرها را حل کنید.
۷. نرم‌افزار
در نرم‌افزارها برای عمل ضرب، تقسیم، و توان، به‌ترتیب از نمادهای *، /،و ^، استفاده می‌شود.
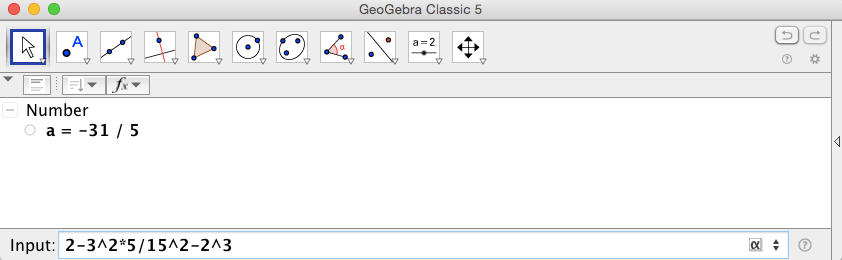
در تصویرهای زیر، جئوجبرا و سایت WolframAlpha حاصل عبارت \(2-3^2\times5\div15^2-2^3\) را محاسبه کرده‌اند و آن را به‌صورت یک کسر ساده‌نشدنی نمایش داده‌اند.
۸. اصطلاحات انگلیسی
اگر اصطلاحات انگلیسی را بدانید، می‌توانید درسنامه‌های دیگری را نیز در سایت‌های انگلیسی زبان بخوانید.
در متن زیر، سعی کنید که معادل اصطلاحات جمع، تفریق، ضرب، تقسیم، توان، و پرانتز را بیابید.
Order of Operations
Do things in Parentheses First\[\begin{aligned}&6\times{\color{red}(5+4)}\\&=6\times{\color{red}9}\\&=54.\end{aligned}\]
Exponents (Powers) before Multiply, Divide, Add or Subtract\[\begin{aligned}&5\times{\color{red}2^3}\\&=5\times{\color{red}8}\\&=40.\end{aligned}\]
Multiply or Divide before you Add or Subtract\[\begin{aligned}&2+{\color{red}5\times7}\\&=2+{\color{red}35}\\&=37.\end{aligned}\]
Otherwise, just go left to right\[\begin{aligned}&{\color{red}30\div5}\times3\\&={\color{red}6}\times3\\&=18.\end{aligned}\]
در ادامه، برای اینکه دوباره اصطلاحات بالا را ببینید، یک تمرین ساده به‌همراه راه‌حل آن آمده است.
What is the value of \(7+(6\times5^2-3)\)?
\[\begin{aligned}{\rm Start\; with}:&\quad7+(6\times5^2-3)\\{\rm Parentheses\;first\;and\;then\;Exponents}:&\quad7+(6\times25-3)\\{\rm Then\;Multiply:}&\quad7+(150-3)\\{\rm Then\;Subtract:}&\quad7+(147)\\{\rm Parentheses\;completed:}&\quad7+147\\{\rm Last\;operation\;is\;an\;Add:}&\quad154.\end{aligned}\]
سلام ۲تا سوال اولویت عملکرد ها می خواستم سخت باشه و با جواب
متشکر
سلام
روی دکمهٔ سبز که در متن هست کلیک کنید تا به تمرینهای بیشتری دسترسی داشته باشید.
سلام، خسته نباشید
خاصیت توزیع پذیری در چه جایگاهی از اولویت عملگرها قرار می‌گیره؟
میشه همتراز با پرانتز در نظر گرفتش؟
سلام
خاصیت توزیع‌پذیری، یعنی عمل ضرب در پرانتزی که در آن جمع یا تفریق وجود دارد. که هم می‌توان ابتدا مقدار داخل پرانتز را محاسبه کرد و حاصل را در عدد بیرون پرانتز ضرب کرد، و هم می‌توان اعداد داخل پرانتز را، جداگانه در عدد بیرون پرانتز ضرب کرد و سپس، حاصل جمع یا تفریق‌ها را محاسبه کرد. فرقی نمی‌کند که از کدام روش استفاده کنید.
خیلی ممنون بابت پاسخ سریع‌تون ❤️
سلام میشه لطفامراحل اولویت بندیشو توضیح بدین؟؟
سلام
در بخش ۲ نوشتهٔ بالا، اولویت‌ها توضیح داده شده است.
خوب بود
با سلام.چرایی این تقدم اعمال را نیز بگویید که به چه علت این ترتیب وجود دارد؟
سلام
صرفاً قرارداد است. و این قرارداد را همه ریاضیدانان پذیرفته‌اند.
با سلام جسارتا روش حل کردن تمرینات اولویت های محاسباتتان در تمرینات اول صفحه با هم تناقض دارند. در تمرین الف با تمرین ج اولویت ها متناقضی هستند.
سلام
لطفاً دقیق‌تر بفرمایید که تناقض در چه چیزی است. در کدام مرحله از محاسبات «الف» یا «ج» تناقضی که می‌فرمایید اتفاق افتاده است؟
سلام میشه از سایر فصل ها و مبحث ها هم بزارید؟
سلام
نوشتن درسنامه‌های مفصل برای همهٔ مباحث مهم، در برنامه‌های آتی سایت تکمیلی هست. به قسمت «درسنامه‌های ریاضی» بروید و در آنجا بقیهٔ درسنامه‌ها را ببینید.
معذرت میخوام اولویت با توان هست یا قدر مطلق؟
قدر مطلق. قدرمطلق مثل پرانتز است.
در یک عملیات ریاضی اول تفریق اومده بعد ضرب،هیچ کدام هم داخل پرانتز نیست،اول تفریق رو انجام میدیم یا ضرب رو؟؟
اول ضرب را انجام می‌دهید.
اولویت ضرب و تقسیم بالاتر از جمع و تفریق است.
سلام اولویت با جمع زیر رادیکاله؟یا رادیکال مثلا
رادیکال 4+5 میشه؟ 3
سلام
درواقع، موجودات زیر رادیکال، داخل پرانتزی با توان \(\frac{1}{2}\) هستند. در ریاضیات سال دهم، می‌خوانید که برای مثال:
\[\begin{aligned}&\sqrt{5+4}&=\big(5+4\big)^{\frac{1}{2}}\\&=9^{\frac{1}{2}}\\&=3.\end{aligned}\]
چطور 3 + 4 شد 9؟
ممنون که تذکر دادید.
اصلاح شد.
جواب منفی 2 در پرانتز به توان 2 زیر رادیکال اول باید رادیکالو حسب کنیم یاتوانو
اول باید توان رو حساب کنید.
توجه کنید که حاصل رادیکال نمی‌تواند عددی منفی شود.
بعضی ها میان همینجور توان و رادیکال رو خط میزنن میگن منفی 2 ولی این غلطه در واقع قدر مطلق باید بگیری وقتی از زیر رادیکال میکشی بیرون جوابش میشه 2
عالییییییییییییییییی بوددددددددددددددد
خیلی ممنون از مطالب زیباتون
ولی سوالی ک اینجا پیش میاد اینکه ما اگه / (تقسیم) خط کسری فرض کنیم نتیجه فرق میکنه!!و مانند نتیجه ای میشه ک اول ضرب رو انجام میدیم
الان کدوم درسته؟!!
اگر به‌جای تقسیم خط کسری بگذاریم، خواهیم داشت:
\[\begin{aligned}&\frac{8}{2}(2+2)\\[7pt]&=\frac{8}{2}(4)\\[7pt]&=4(4)\\[7pt]&=16.\\\end{aligned}\]
پس اگر به‌جای \(\div\) از خط کسری استفاده کنیم، حاصل عبارت فرقی نمی‌کند.
صحیح
ولی چرا بعد ۸ زیر خط کسری کل عبارت رو قرار نمیدین؟!
چون در اون‌صورت باید کل عبارت بعد از \(\div\)، داخل پرانتز می‌بود:
\[8\div\big(2(2+2)\big)=\frac{8}{2(2+2)}\]
😂😅🤦♂️
مرسی ممنون اینو یادم رفته بود
سلام حاصل این سوال چیست 4+6-10
\[\begin{aligned}&10-6+4\\&=4+4\\&=8.\end{aligned}\]
ببخشید من خواستم تو آزمونک شرکت کنم، ولی همچین چیزی نمایش داده میشه
\(8-4\times3\div2-6\)
\(4^2-3^2-16\div4\)
الان که من چک کردم مشکلی نبود.
اگر با چنین مواری برخورد کردید، صفحه را رفرش کنید. اگر پس از چندبار رفرش، مشکل حل نشد، لطفاً اطلاع بدید.
بله الان امتحان کردم درست شد، ممنونم.
مطالب خیلی عالی بود همرو کامل متوجه شدم آزمون هم عالی
این مثال هایی ک زدین درست نیس ، درسته ک باید عملگر های مساوی رو از چپ ب راست حل کرد اما زمانی ک پرانتز رو حل کردین یک عدد ک تو پرانتز موند نباید پرانتزش برداشته بشه تا اول اون محاسبه بشه
مثلا (2*2)8/2میشه 2 ضربدر 2 میشه 4 که 4 هنوز تو پرانتزه بعدش اول 2*4 میشه در اخر 8 برش تقسیم میشه ک جوابش 1 میشه
همان‌طور که در متن درس توضیح داده شده است، وقتی دو عمل اولویت یکسانی داشته باشند، باید از چپ به راست عملیات را انجام دهید. بنابراین، پاسخ آن مسئله برابر \(1\) نیست و پاسخ درست \(16\) است. و راه‌حل تشریحی آن در متن درس هست.
کاملا با امیر موافقم و پاسخی که شما دادید را اشتباه میدونم. ضرب با پرانتز ،ضرب ضمنی محسوب میشه و شما حق نداشتید پرانتز را حذف و به جای آن یک علامت ضرب معمولی بگذارید.
ضمنا ضرب ضمنی به مراتب اولویتش بیشتر از آن علامت تقسیم است که در سمت چپ آمده.
بطور کلی وقتی پرانتز در عبارت ریاضی وجود داره ، اول باید هر آنچه با پرانتز درگیر است محاسبه شود تا پرانتز بطور کامل از بین بره. بعد میتونید باقی محاسبات را انجام دهید.
M÷N×P با M÷N(P) کاملا متفاوت است.
لطفا در این مورد به کتاب لاندائو مراجعه کنید.
توجه کنید که اولویت عملگرها صرفاً یک قرارداد است. ممکن است شخصی کتابی بنویسد و در آن، اولویت‌ها را جور دیگری تعریف کند. اما آنچه که مرسوم است و همهٔ نرم‌افزارهای مهم نیز از آن تبعیت می‌کنند، همان است که در درسنامهٔ بالا گفته شده است.
درگزینه د چرا به جای 4به توان 6 نوشتید 4 به توان 9؟ مگه توانها در هم ضرب نمیشن؟
در \(4^{3^2}\)، اولویت با توان است. پس ابتدا \(3\) به توان \(2\) می‌رسد که حاصل میشه \(9\)؛ و بعد \(4\) به توان \(9\) می‌رسد.
در \(\big(4^3\big)^2\)، اولویت با پرانتز است. پس ابتدا \(4\) به توان \(3\) می‌رسد که حاصل میشه \(64\)؛ و بعد \(64\) به توان \(3\) می‌رسد.
دربارهٔ آنچه می‌گویید توانها در هم ضرب می‌شوند، فقط برای \(\big(4^3\big)^2\) برقرار است. چون با توجه به تعریف توان داریم:
\[\begin{aligned}\big(4^3\big)^2&=\big(4^3\big)\big(4^3\big)\\&=4^{3+3}\\&=4^{3\times2}\\&=4^6.\end{aligned}\]
در \(4^{3^2}\)، با توجه به تعریف توان داریم:
\[4^{3^2}=4^{3\times3}=4^9.\]
مثال گزينه ب
پاسخ رو اشتباه نوشتين چون موقع پاسخ صورت مسئله رو عوض كردين
اصلاح شد.
با سپاس فراوان از شما که تذکر دادید.