در بسیاری از کلاسهای ریاضی، در مبحث توان، این سؤال پیش میآید که «صفر به توان صفر چیست؟» و معمولاً بحث و نتیجهگیری دربارهٔ آن، برای همه قانعکننده نیست. بسیاری از افراد، کتابها، و وبسایتها اظهار نظرهایی دربارهٔ صفر به توان صفر کردهاند. اما یک محقق واقعی وقتی میخواهد پاسخی مناسب برای چنین مسائلی بیابد، ابتدا تاریخچه و بحثهای ریاضیدانان گذشته را میخواند، سپس، نظر ریاضیدانان بزرگ معاصر را نیز جویا میشود، و در نهایت، پس از اینکه به جمعبندی مناسبی رسید، دربارهٔ آن مسئله اظهار نظر میکند.
در زیر، ابتدا ویدئویی از توضیحات دو ریاضیدان معاصر را دربارهٔ صفر به توان صفر میبینید. سپس، ترجمهٔ یکی از مقالههای مفصل دربارهٔ صفر به توان صفر را، که در سال \(2012\) منتشر شده است، خواهید خواند.
توضیحات دو ریاضیدان دربارهٔ صفر به توان صفر
تقسیم بر صفر چیست؟ صفر به توان صفر چیست؟
مت پارکر (Matt Parker)، و جیمز گریم (James Grime) در ویدئوی زیر، به این پرسشها پاسخ میدهند.
در ادامه، قبل از اینکه ترجمهٔ مقالهٔ مفصل «\(\rm What\;is\;0^0?\)» را بخوانید، میتوانید خلاصهای از این مقاله را در اینستاگرام تکمیلی ببینید.
صفر به توان صفر چیست؟
نوشتهٔ میشل هوبر (Michael Huber) و فردریک ریکی (Frederick Rickey)
منتشر شده در وبسایت انجمن ریاضی آمریکا (Mathematical Association of America)
مقدمه
وقتی در کتابهای حسابان (calculus) گفته میشود که \(0^0\) یک صورت مبهم است، یعنی دو تابع \(f(x)\) و \(g(x)\) وجود دارند بهطوریکه \(f(x)\) و \(g(x)\) هر دو به سمت صفر میل میکنند و باید حاصل عبارت زیر محاسبه شود.
\[\lim_{x\to0}\big(f(x)\big)^{g(x)}\] اما اگر \(0\) تنها یک عدد باشد چه؟ در چنین حالتی، برخلاف آنچه که اغلب کتابهای درسی میگویند، \(0^0\) کاملاً خوشتعریف است؛ و در حقیقت داریم: \[0^0=1.\]
کتابهای درسی در عصر حاضر
در اکثر کتابهای ریاضی دبیرستانی، صفر به توان صفر به عنوان یک صورت مبهم در نظر گرفته شده است. برای مثال، متن زیر در یک کتاب درسی ریاضی که در یکی از نواحی نیویورک تدریس میشود، آمده است:
\[x^a\div x^b=x^{(a-b)}\quad (x\ne0)\] اگر در عبارت بالا، شرط \(a > b\) را نداشته باشیم، و \(a=b\)، آنوقت داریم:
\[\begin{aligned}&x^a\div x^b\\&=x^a\div x^a\\&=x^{(a-a)}\\&=x^0\end{aligned}\] اما \[x^a\div x^a=1\] بنابراین، برای بامعنی بودن \(x^0\) باید تعریف کنیم:\[x^0=1.\quad(x\ne0)\] چون تعریف \(x^0\) براساس تقسیم بنا شده و تقسیم بر صفر ممکن نیست، باید فرض کنیم \(x\ne0\). درواقع، عبارت صفر به توان صفر یکی از صورتهای مبهم در ریاضی است و غیرممکن است که یک مقدار را به یک عبارت مبهم نسبت داد.
در کتابهای حسابان استدلال زیر نوشته شده است:
اما این پرسش پیش میآید:
«آیا میتوان بین \(0^0\) حدی، و \(0^0\) بهعنوان یک عدد، فرق گذاشت؟»
بحث دربارهٔ صفر به توان صفر
رفتار \(0^0\) چندصد سال است که مورد بحث بوده است. لئونار اویلر (Leonhard Euler)، در کتاب «اصول جبر خود» در سال \(1770\)، چنین نوشته است:
اویلر در سال \(1748\) در کتابی با عنوان «مقدمهای بر آنالیز بینهایت»، نوشته است:
اگر \(z=0\)، آنگاه \(a^0=1\). اگر \(a=0\)، آنگاه در مقدار \(a^z\) پرشی بزرگ داریم. تا زمانی که مقدار \(z\) مثبت باشد، داریم \(a^z=0\). اگر \(z=0\)، آنگاه \(a^0=1\).
اویلر لگاریتم \(y\) را تابعی از \(z\) تعریف کرده بهطوریکه \(a^z=y\). او با نوشتن جملهٔ «میدانیم مبنای لگاریتم باید عددی صحیح و بزرگتر از \(1\) باشد»، از مشکل احتمالی \(0^0\) فرار کرده است.

تعریف توان، اغلب با بیدقتی انجام شده است. جرج بارون در سال \(1804\)، مقالهای منتشر کرد که با این تعریف آغاز میشد: «توانهای هر عدد، عبارت است از ضربهای متوالی که از عدد \(1\) شروع شده و بهطور مستمر، آن عدد در خودش ضرب میشود.»
بهعنوان مثال، او نوشته: «\(5^1=1\times5\) و \(5^2=1\times5\times5\) و همینطور تا آخر. به همین روش، توانهای هر عدد، مانند \(x\)، را میتوان بهصورت
\[\begin{aligned}x^1&=1\times x\\x^2&=1\times x\times x\\x^3&=1\times x\times x\times x\\\vdots&\end{aligned}\] نمایش داد.»
بارون پس از بیان چند نتیجه، گفت: «آیا تعریف مشابهی ما را به یک راهحل دقیق و قابل درک برای آنچه که توان هیچاُم (توان صفر) اعداد نامیده شده، راهنمایی نمیکند؟» و برای پاسخ به سؤال خود، از قوانین تقسیم توان (که در کتابهای دبیرستانی امروزی نیز هستند) اشاره کرد؛ اما یک نتیجهٔ متفاوت ارائه کرد:
\[\frac{x^1}{x}=\frac{1\times x}{x}=1\] یعنی \(x^0=1\). چون در اینجا، \(x\) یک عدد دلخواه است، پس توان هیچاُم هر عدد، برابر \(1\) است.
در آن مقاله، بارون نوشتههای ویلیام امرسون (William Emerson) و جارد منسفیلد (Jared Mansfield) را دربارهٔ «هیچ» تأیید کرد و بحثهای آن دو را یک پله جلوتر برد، و ادعا کرد که عدد \(x\) میتواند هر عدد خیلی بزرگ یا خیلی کوچک باشد. او نوشت:
البته بارون هیچ اشارهای به صورت مبهم نمیکند و مقالهٔ خود را با این توضیح به پایان میرساند: «چون برای هر مقدار \(x\) داریم \(x^0=1\)، در نتیجه، لگاریتم \(1\) در هر مبنایی برابر \(0\) است.»
دونالد کنوث در صفحهٔ ۶ مقالهٔ «Two Notes on Notation»، به تاریخچهٔ بحثهای ریاضیدانان قرن نوزدهم، دربارهٔ \(0^0\) پرداخته است:
اما نه، نه، دههزار بار نه! هر کسی قضیهٔ دوجملهای
\[(x+y)^n=\sum_{k=0}^n\binom{n}{k}x^ky^{n-k}\] را پذیرفته باشد، باید به \(0^0=1\) معتقد باشد؛ زیرا با جایگذاری \(x=0\) و \(y=1\) در قضیهٔ دوجملهای، طرف چپ آن برابر \(0^0\) و طرف راست آن برابر \(1\) است.
از طرفی، کوشی استدلال خوبی برای تعریف نشده بودن صورت حدی \(0^0\) ارائه کرد. او گفت که اگر \(f(x)\) و \(g(x)\) بهطور مستقل به سمت صفر میل کنند، آنگاه حد \(\big(f(x)\big)^{g(x)}\) ناشناخته است. اما تعریف مقدار \(0^0\) راحتتر از این است که بخواهیم \(0+0\) را تعریف کنیم. کوشی و لیبری، هر دو درست میگفتند؛ اما لیبری و مدافعانش نمیدانستند که چرا حق با آنهاست.
چند مثال
در سال \(1970\)، هربرت واون (Herbert Vaughan) در مقالهای با عنوان «عبارت \(0^0\)»، برای به رسمیت شناختن \(0^0=1\) سه مثال زیر را ارائه کرد.
مثال ۱. فرض کنید \(|x| < 1\). در سری هندسی \[\sum_{n=1}^{\infty}x^{n-1}=\frac{1}{1-x}\quad (1)\]برای \(x=0\) داریم: \[\begin{aligned}&\sum_{n=1}^{\infty}0^{n-1}=\frac{1}{1-0}\\&\Rightarrow0^0+0^1+0^2+0^3+\dots=1.\end{aligned}\] به گفتهٔ واون، اگر \(0^0\) مبهم باشد، سری بالا نیز بیمعناست. علاوه بر آن اگر \(0^0\ne1\)، آنگاه رابطهٔ \((1)\) نادرست است.
مثال ۲. میدانیم که برای هر \(x\)،
\[\sum_{n=1}^{\infty}\frac{x^{n-1}}{(n-1)!}=e^x.\quad(2)\]
همه پذیرفتهاند که \(0!=1\). بنابراین، اگر در رابطهٔ \((2)\) قرار دهیم، \(x=0\) داریم:
\[\begin{aligned}&\sum_{n=1}^{\infty}\frac{x^{n-1}}{(n-1)!}=e^0\\[7pt]&\Rightarrow\frac{0^0}{0!}+\frac{0^1}{1!}+\frac{0^2}{2!}+\dots=1\\[7pt]&\Rightarrow\frac{0^0}{1}=1\\[7pt]&\Rightarrow0^0=1.\end{aligned}\]
مثال ۳. واون در سومین مثال، از مفهوم عدد اصلی (cardinal number) در نظریهٔ مجموعهها استفاده میکند. در اینجا، این مثال را با زبانی سادهتر شرح میدهیم.
فرض کنید \(A\) یک مجموعهٔ \(a\)عضوی و \(B\) یک مجموعهٔ \(b\)عضوی باشد. \(A^B\) مجموعهٔ همهٔ توابع از \(B\) به \(A\) است. تعداد این توابع برابر است با \(a^b\). برای مثال، اگر \(A=\{1,2\}\) و \(B=\{x,y,z\}\)، آنگاه \(a^b=2^3\)، زیرا
\[\begin{aligned}A^B=\Big\{&\big\{(x,1),(y,1),(z,1)\big\},\\&\big\{(x,1),(y,1),(z,2)\big\},\big\{(x,1),(y,2),(z,1)\big\},\big\{(x,2),(y,1),(z,1)\big\},\\&\big\{(x,1),(y,2),(z,2)\big\},\big\{(x,2),(y,1),(z,2)\big\},\big\{(x,2),(y,2),(z,1)\big\},\\&\big\{(x,2),(y,2),(z,2)\big\}\Big\}.\end{aligned}\] تعداد توابع از یک مجموعهٔ تهی به یک مجموعهٔ تهی باید برابر با \(0^0\) باشد. از یک مجموعهٔ تهی به یک مجموعهٔ تهی فقط یک تابع وجود دارد: تابع تهی. در نتیجه، \(0^0=1\).
یک ریاضیدان در چه مواردی ممکن است بخواهد که صفر به توان صفر مبهم نباشد؟
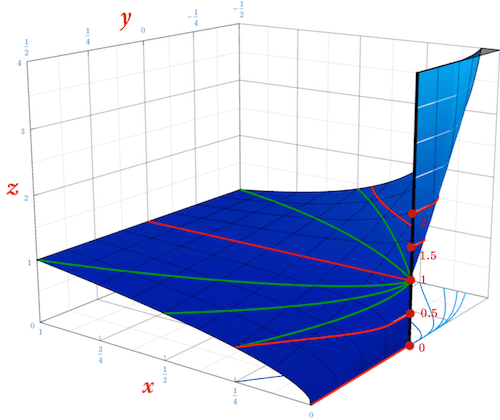
نمایش یک تابع. تابع \(f\,(x,y)=x^y\) را در نظر بگیرید. صرفنظر از اینکه چه مقداری را به \(0^0\) نسبت دهیم، تابع \(x^y\) نمیتواند در \(x=y=0\) پیوسته باشد، چون حد \(x^y\) در امتداد خط \(x=0\) برابر \(0\) است؛ اما حد \(x^y\) در امتداد خط \(y=0\) برابر \(1\) است. پس یک انتخاب منطقی و طبیعی این است که \(0^0\) برابر با \(1\) تعریف شود.
نتیجهگیری
اگر شما با حد کار میکنید، آنگاه \(0^0\) یک صورت مبهم است. اما اگر با جبر معمولی سر و کار دارد، آنگاه \(0^0=1\).
نظر شما دربارهٔ صفر به توان صفر چیست؟







نمیتونیم بگیم که وقتی ما هیچی رو به توان هیچی نمیرسونیم میشه 0؟
0^0 یعنی اینکه صفر بخش از یک کیک رو به صفر نفر تقسیم کنیم، که یعنی درواقع ما هیچ کاری نکردیم و جواب صفره
تعریف اولیه توان، برای وقتی است که توان عددی طبیعی است.
حالتهای دیگر باید تعریف شوند و نمیتوان از چنین تفسیرهایی استفاده کرد.
در ریاضیات،
\(\bullet\) توان صفر، تعریف دارد.
\(\bullet\) توان منفی، تعریف دارد.
\(\bullet\) توان گویا، تعریف دارد.
\(\bullet\) و توان گنگ هم تعریف دارد.
حتماً درسنامه توان سایت تکمیلی را بخوانید.
سلام و خسته نباشید
در قسمت اصول جبر اویلر ۱۷۷۰، وقتی گفته میشه حتی اگر هیچ باشه، خب ما یه کسر صفر صفرم نداریم؟ چجوری اینجا توجیه شده؟
یا مثلا بخش بارون (کمی قبل امرسون)، این عدد دلخواه اگر صفر باشه طبق رابطهی بالا، بازم کسر صفر صفرم داریم.
خب این استفاده از تقسیم نیست و صفر صفرم تعریف نشده نیست؟
و اینکه من با استفاده از تساوی $0^0=1$، به تناقض میرسم.
$\frac{0^0}{0^0}=\frac{1}{1}=1$
اما از طرفی:
$\frac{0^0}{0^0}=(\frac{0}{0})^{0}$
خب صفر صفرم تعریف نشده هستش و به توان صفرش هم همینطور.
چطور این کسر ما همزمان حاصلش یکه و همزمان تعریف نشدس؟
سلام
دربارهٔ اویلر و بارون که نوشته شده آنها از صورتهای مبهم فرار کردهاند.
آن تساوی آخری که شما نوشتهاید، تناقض ندارد؛ چون شما فکر میکنید قوانین توان باید همهجا کار کنند و هیچ شرطی برای آنها قائل نیستید، فکر میکنید به تناقض رسیدهاید.
هر چقدر از عالی بودن سایتتون بگم کمه پاسخنامه های تکمیلی واقعا تشریحی هستند و بخش های ویدیو های کوتاه/درسنامه هفته مسئله های اینایا خیلی جالب و کامل هستند
خدا قوت
ممنون از شما
سپاس از انرژی مثبتی که به ما میدهید.
سعی میکنیم با همراهی شما عزیزان، مطالب مفید بیشتری تولید کنیم.
عالی بود
ویدیو عالی بود
کاش بعضی ها اول مطلب رو میخوندند بعد اگه چیزی فهمیدند میگفتند
با این نظریه های خفنی که توسط دکتران داده شد موریس کلاین داره خودزنی میکنه
صفر به توان صفر یعنی صفر رو صفر بار در خودش ضرب کنیم یعنی جواب خود صفر
خیر اینطور نیست. اگر اینجوری است چرا n^0 = 1 ( n!=0) ؟
از دو بعد میشه به مسعله نگاه کرد
بعد اول نظریه جواب ما مبهم است چون چیزی نداریم که توان صفر را برایش اجرا کنیم
اما بعد دووم به ما اثبات میکنه که برا هیچ چیز همه چیزو در نظر بگیریم
از این رو اگر دوجواب رو القا کنیم نظریه ی اول منطقی تر نسبت به دومیست
عالی بود ممنون از لطفتون
فقط صفر به توان صفر یا تقسیم بر صفر مبهم است.
صفر به توان صفر مبهم است.چون هیچ چیز ندارید که به توان 0 برسانید
۳¹=۳
۲¹=۲
۱¹=۱
۰¹=۰
پس نتیجه میشود صفر به توان یک است
کاش نوشته رو میخوندی بعد نظر میدادی
واقعا جالب بود ویدیو
ویدیوتون خیلی جذاب بود ، ممنونم که این اطلاعات رو در اختیارمون گذاشتین ??????
جالب بود